CS2205_PLDI

CS2205 Programming Language Design and Implementation

1. Background

程序设计语言的发展：机器语言 → 汇编语言 → 高级语言

编译器的作用：把某一种高级语言程序等价地转换成另一种低级语言程序

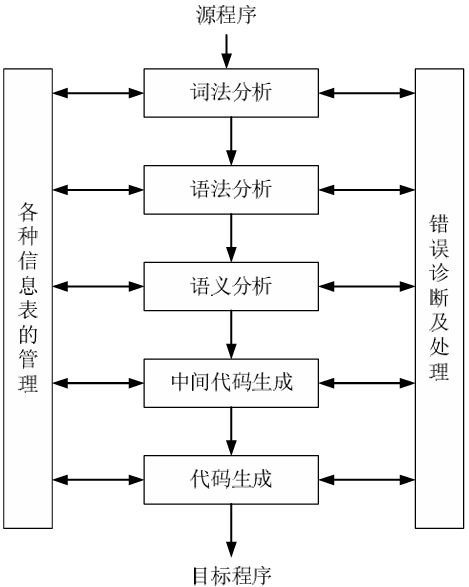
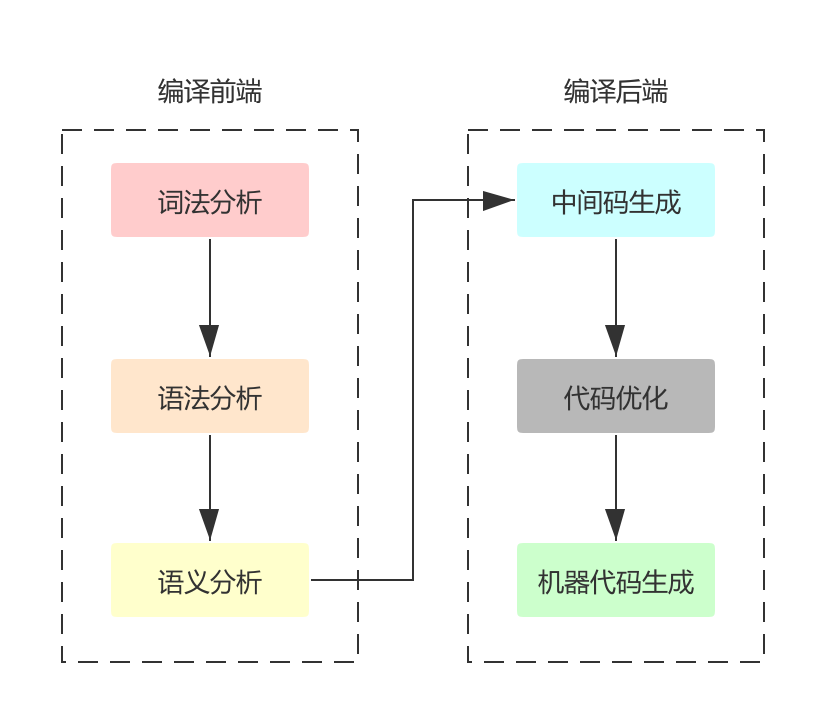
编译程序的工作过程大致可以分为五个阶段：词法分析、语法分析、语义分析和中间代码生成、代码优化、目标代码生成。

1. 词法分析 (lexical analysis) : 对构成输入源程序的字符串进行扫描和分解，识别出一个个单词符号，即 token，如标识符、常数、界限符等。

2. 语法分析 (syntax analysis) : 在词法分析的基础上，根据语言的语法规则，把单词符号分解成各类语法单位（语法范畴），如：”短语”、”句子”、”子句”、”程序段” 等。输出是一棵抽象语法树 (Abstract Syntax Tree)。

3. 语义分析 (semantic analysis) 和中间代码 (Intermediate Representation) 生成：首先对各种语法范畴进行静态语义检查，如果正确则进行中间代码的翻译。该阶段遵循的是语言的语义规则，通常使用属性文法描述语义规则。中间代码的形式有：四元式、三元式、间接三元式、逆波兰记号和树形表示。

   以三地址码，一种比较简单且常见的中间表示为例：

   a = b + c * d;
       ↓↓
   t1 = c * d;
   a = b + t1;

4. 代码优化：从抽象语法树到中间代码，更多考虑的是如何对语句进行等价转换，代码的效率不是主要考虑因素。为了最终生成的程序能够更高效的执行和存储，现代编译器往往会花很大力气去对代码进行优化，而且会不止一次地对代码进行扫描和优化。优化所依循的原则是程序的等价变换规则。其方法有：公共子表达式的提取、循环优化、删除无用代码等。

5. 目标代码生成：以优化后的中间代码作为输入，产生等价的目标代码作为输出。它有赖于硬件系统结构和机器指令含义。如何充分利用寄存器、合理选择指令以生成尽可能短且有效的目标代码等都与目标机器硬件结构有关。

2. Compiler Front-end Task

【编译器前端】词法规则文本的词法分析、语法分析与 DFA 生成

​ 在使用 Flex 词法分析工具时，”.l” 文件包含用正则表达式表示的词法分析规则与 C 程序编写的处理程序。参考这一格式，设计一种词法规则文本的格式，也包括正则表达式（用含转义符号的字符串表示）与 WhileDeref 程序。任务要求如下：

1. 完成词法规则问题的词法分析、语法分析与语法树输出。
2. 由正则表达式生成 NFA，并输出。
3. 进一步生成 DFA，并输出。

3. While 语言

​ 下面定义了一个简单的程序语言 while 语言。

• 常数

  • N ::= 0 | 1 | ...
  • While 语言的常数是以非 0 数字开头的一串数字或者 0。

• 保留字

  • While 语言的保留字有：var, if, then, else, while, do

• 变量名

  • V ::= ...
  • While 语言变量名的第一个字符为字母或下划线，while 语言的变量名可以包含字母、下划线与数字。例如：a0，__x， leaf_counter 等等都可以是 while 语言的变量名。
  • 保留字不是变量名。

• 表达式

  • E :: = N | V |-E | E+E | E-E | E*E | E/E | E%E |

    E<E | E<=E | E==E | E!=E | E>=E | E>E |

    E&&E | E||E | !E

  • 优先级：|| < && < ! < Comparisons < +,- < *,/,%

  • 同优先级运算符之间左结合，可以使用小括号改变优先级。例如：a0+1，x<=y&&x>0 等等都是 while 语言的表达式。

• 语句

  C :: = var V |
  V = E |
  C; C |
  if (E) then { C } else { C } |
  while (E) do { C }

  4. While 语言 + Dereference + Built-in functions

• 表达式

  E :: = N | V |-E | E+E | E-E | E*E | E/E | E%E |
  E<E | E<=E | E==E | E!=E | E>=E | E>E |
  E&&E | E||E | !E | *E |
  malloc(E) | read_int() | read_char()

• 语句

  C :: = var V |
  write_int(E) |
  write_char(E) |
  E = E |
  C; C |
  if (E) then { C } else { C } |
  while (E) do { C }

• While 程序示例 1

  var x;
  var n;
  var flag;
  x = read_int();
  n = 2;
  flag = 1;
  while (n * n <= x && flag) do {
  if (x % n == 0)
  then { flag = 0 }
  else { n = n + 1 }
  };
  write_int(flag)

5. Flex 词法分析

​ 在 While+DB 语言中有以下几类标记 (token)：

• 运算符：+ - * / % < <= == != >= > ! && ||

• 赋值符号：=

• 间隔符：( ) { } ;

• 自然数：0 1 2 ...

• 变量名：a0 __x ...

• 保留字：var if then else while do ...

• 内置函数名：malloc read_char read_int write_char write_int

​ 下面是 lang.l 文件中的词法规则部分，每条规则都由 pattern 和 action 组成：

1. pattern 使用正则表达式表示，含义为需要匹配的词的规则。
2. action 使用代码表示，含义为成功匹配该词后执行的动作。

%%
0|[1-9][0-9]* {	// 自然数
    yylval.n = build_nat(yytext, yyleng);	// 需额外存储对应值
    return TM_NAT;
}

"var" {	// 保留字
    return TM_VAR;
}

...	// 省略部分保留字

"return" {
    return TM_return;
}

"func" {	// 函数名
    return TM_func;
}

"proc" {
    return TM_proc;
}

[_A-Za-z][_A-Za-z0-9]* {	// 标识符
    yylval.i = new_str(yytext, yyleng);
    return TM_IDENT;
}

";" {	// 间隔符
    return TM_SEMICOL;
    }

...	// 省略部分间隔符

"}" {
    return TM_RIGHT_BRACE;
    }

"+" {	// 运算符
    return TM_PLUS;
    }

...	// 省略部分运算符

"!=" {
    return TM_NE;
    }

"=" {	// 赋值符
    return TM_ASGNOP;
    }

[ \t\n\r]    { };	// 空白字符

.   {printf("%s",yytext);
     return -1; }
%%

​ 为了对于上面的词法规则进行词法分析、语法分析，我们可以将每一条规则-动作视作一条匹配语句：每个 pattern 都对应有一个 rules。根据上面 pattern 定义的识别规则，可以抽象成以下五种类型：

1. 自然数正则规则：pattern：0|[1-9][0-9]*；及对应的 rules；
2. 标识符正则规则：pattern：[_A-Za-z][_A-Za-z0-9]*；及对应的 rules；
3. 空白字符正则规则：pattern：[ \t\n\r]；及对应的 rules；
4. 关键字正则规则：pattern："[_A-Za-z][_A-Za-z0-9]*"（通过双引号来区别于标识符规则，函数名这里也将其视为一种关键字）；及对应的 rules；
5. 符号正则规则：pattern："[^A-Za-z0-9_]{1,2}"（我这里将运算符、分隔符、赋值符均统一成相同的符号正则）；及对应的 rules；

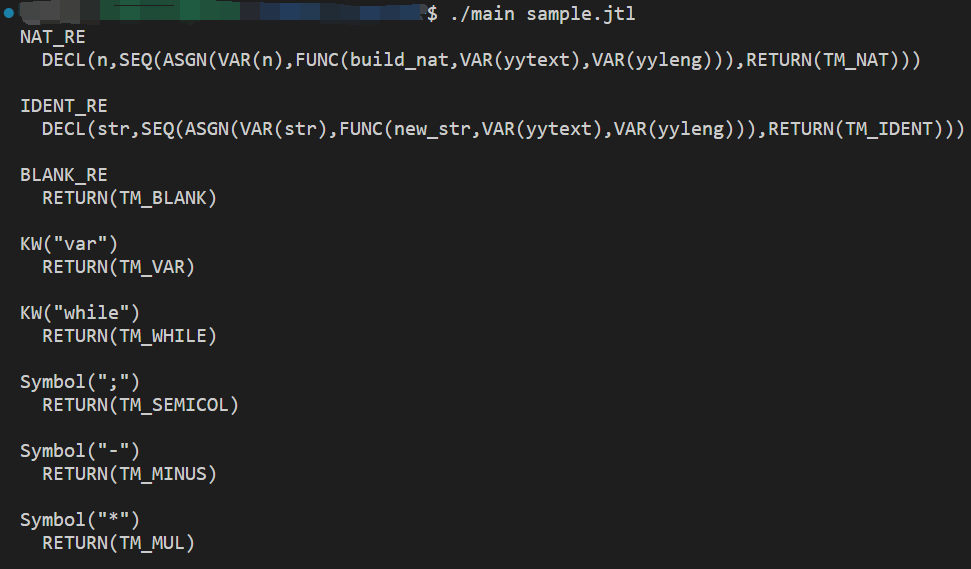
​ 在 lang.l 中增添以下规则：

"0|[1-9][0-9]*" {	// 识别自然数正则规则
    return TM_NAT_RE;
}

"[_A-Za-z][_A-Za-z0-9]*" {	// 识别标识符正则规则
    return TM_IDENT_RE;
}

"[ \\t\\n\\r]" {	// 识别空白字符正则规则
    return TM_BLANK_RE;
}

\"[_A-Za-z][_A-Za-z0-9]*\" {	// 识别关键字正则
    yylval.i = new_str(yytext, yyleng);	// 额外存储关键字的字符串信息
    return TM_KEYWORD;
}

\"[^A-Za-z0-9_]{1,2}\" {	// 识别符号正则
    yylval.i = new_str(yytext, yyleng);
    return TM_SYMBOL;
}

​ 使用 Flex 工具进行词法分析

Flex 生成的词法分析器的算法流程如下：先根据输入的字符串找到正则表达式的匹配结果（若有多种结果则选最长、最靠前的），再更新字符串扫描的初始地址，并执行匹配结果对应的处理程序。

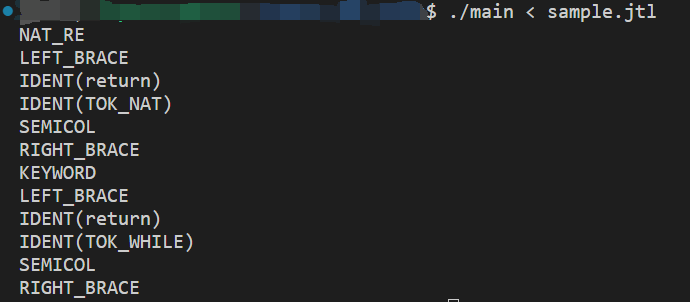
• 测试文本文件 sample.jtl 如下：

  0|[1-9][0-9]* { 
      return TOK_NAT; 
  }
  
  "while" {
      return TOK_WHILE;
  }

• 词法分析结果：

  

6. Bison 语法分析

​ 在 flex 成功识别每一个 token 之后，还需要使用 bison 将这些 token 按照规则不断归约，最后变成程序段。

​ bison 运行流程如下：

​ bison 的代码框架和 flex 完全一致，格式都是：

定义(definations)
%%
规则(rules)
%%
代码(user code)

​ 只不过在定义和规则部分，一些写法不同。bison 基于 BNF 定义的规则：rule → BNF action，对于 BNF 中每一个归约方法/产生式，都可以写上 action（花括号括起来）。

​ 下面给出 lang.y 文件增添的主要内容：

%%
%union {
unsigned int n;
char * i;
struct expr * e;
struct cmd * c;
struct glob_item * g;
struct glob_item_list * f;
struct expr_list * h;
struct var_list *k;
void * none;
}

// Terminals
%token <i> ... TM_KEYWORD TM_SYMBOL
%token <none> ... TM_NAT_RE TM_IDENT_RE TM_BLANK_RE

NT_gi:
  ...
| TM_NAT_RE TM_LEFT_BRACE NT_CMD TM_RIGHT_BRACE
  {
    $$ = (TNatReDef($3));
  }
| TM_IDENT_RE TM_LEFT_BRACE NT_CMD TM_RIGHT_BRACE
  {
    $$ = (TIdentReDef($3));
  }
| TM_BLANK_RE TM_LEFT_BRACE NT_CMD TM_RIGHT_BRACE
  {
    $$ = (TBlankReDef($3));
  }
| TM_KEYWORD TM_LEFT_BRACE NT_CMD TM_RIGHT_BRACE
  {
    $$ = ((TKeyWordDef($1, $3)));
  }
| TM_SYMBOL TM_LEFT_BRACE NT_CMD TM_RIGHT_BRACE
  {
    $$ = ((TSymbolDef($1, $3)));
  }
;
%%

​ 在 lang.h 中添加对应的函数声明

struct glob_item * TNatReDef(struct cmd * body);
struct glob_item * TIdentReDef(struct cmd * body);
struct glob_item * TBlankReDef(struct cmd * body);
struct glob_item * TKeyWordDef(char * name, struct cmd * body);
struct glob_item * TSymbolDef(char * name, struct cmd * body);

​ 在 lang.c 中给出上述函数对应的实现，同时添加一些有关输出的处理逻辑即可。

struct glob_item * TNatReDef(struct cmd * body) {
  struct glob_item * res = new_glob_item_ptr();
  res -> t = T_NAT_RE_DEF;
  res -> d.NAT_RE_DEF.body = body;
  return res;
}

struct glob_item * TIdentReDef(struct cmd * body) {
  struct glob_item * res = new_glob_item_ptr();
  res -> t = T_IDENT_RE_DEF;
  res -> d.IDENT_RE_DEF.body = body;
  return res;
}

struct glob_item * TBlankReDef(struct cmd * body) {
  struct glob_item * res = new_glob_item_ptr();
  res -> t = T_BLANK_RE_DEF;
  res -> d.BLANK_RE_DEF.body = body;
  return res;
} 

struct glob_item * TKeyWordDef(char * name, struct cmd * body) {
  struct glob_item * res = new_glob_item_ptr();
  res -> t = T_KW_DEF;
  res -> d.KW_DEF.name = name;
  res -> d.KW_DEF.body = body;
  return res;
}

struct glob_item * TSymbolDef(char * name, struct cmd * body) {
  struct glob_item * res = new_glob_item_ptr();
  res -> t = T_SYMBOL_DEF;
  res -> d.SYMBOL_DEF.name = name;
  res -> d.SYMBOL_DEF.body = body;
  return res;
}

​ 我的 Makefile 文件

lexer.h: lang.l
	flex lang.l

lexer.c: lang.l
	flex lang.l

parser.c: lang.y
	bison -o parser.c -d -v lang.y

parser.h: lang.y
	bison -o parser.c -d -v lang.y

lib.o: lib.c lib.h
	gcc -c lib.c

lang.o: lang.c lang.h lib.h
	gcc -c -g lang.c

parser.o: parser.c parser.h lexer.h lang.h
	gcc -c -g parser.c

lexer.o: lexer.c lexer.h parser.h lang.h
	gcc -c -g lexer.c

main.o: main.c lexer.h parser.h lang.h
	gcc -c -g main.c

main: lang.o parser.o lexer.o lib.o main.o
	gcc lang.o parser.o lexer.o lib.o main.o -g -o main

all: main

clean:
	rm -f lexer.h lexer.c parser.h parser.c *.o main

%.c: %.y

%.c: %.l

.DEFAULT_GOAL := all

​ 使用 Bison 工具进行语法分析

• 测试文本文件 sample.jtl 如下：

0|[1-9][0-9]* {
  var n; 
  n = build_nat(yytext, yyleng);
  return TM_NAT
};

[_A-Za-z][_A-Za-z0-9]* {
  var str; 
  str = new_str(yytext, yyleng);
  return TM_IDENT
};

[ \t\n\r] { 
  return TM_BLANK
};

"var" {
  return TM_VAR
};

"while" {
    return TM_WHILE
};

";" {
    return TM_SEMICOL
};

"-" {
    return TM_MINUS
};

"*" {
    return TM_MUL
}

​ 语法分析结果：

7. 正则→NFA→DFA

（1）从中缀表达式转换为后缀表达式

​ 首先要在转换前进行预处理：在正则表达式中添加连接符号 +，因为正则表达式中的连接运算是隐含的，没有明确的符号表示，例如 ab 表示 a 和 b 的连接，但是在中缀转后缀的过程中，需要有一个明确的符号来表示连接运算的优先级，否则会导致歧义或错误。例如 a(a|b)* 加 + 后的表达式为 a+(a|b)*，表示 a 和 (a|b)* 是拼接起来的。

​ 此外，如果输入的 Regular_Expression 是 string 类型，则当遇到操作符 [...] 指定一个字符集时，此时并不知道具体要匹配哪一个字符，需要用 string 类型暂时存储，而这时会与同为 string 类型的 Regular_Expression 发生冲突，因此还需要将 Regular_Expression 转为 vector<string> 类型。

（2）从后缀表达式转换为 NFA

​ 在正式转换之前，还需要定义一些基本单元（结构体）：node、egde、elem、DFAState、DFATransition

struct node
{
    // 为了便于后修扩展，这里使用结构体存储节点信息，也可以直接使用 string 类型表示 node。
	string nodeName;
};

struct edge
{
	node startName;
	node endName;
	string tranSymbol;
};

// NFA的组成单元，一个大的 NFA 单元可以是由很多小单元通过规则拼接起来
struct elem
{
	int edgeCount;
	edge edgeSet[100];
	node startName;
	node endName;
};

// 定义 DFA 的状态
struct DFAState {
	set<string> nfaStates;	//一个包含NFA状态的集合
	string stateName;
};

// 定义 DFA 的转换关系
struct DFATransition {
	DFAState fromState;
	DFAState toState;
	string transitionSymbol;
};

​ 转换使用 Thompson 构造法

1. 递归终点

   对于正则表达式为 ε 或只有一个符号构成的情况，则无需递归，

   

2. 子表达式运算的构造规则

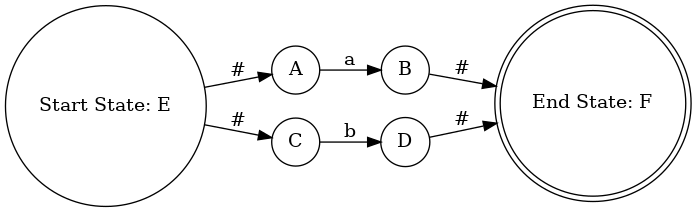
   1. 或运算 a|b 的构造

      

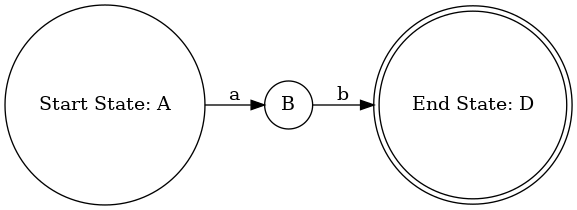
   2. 连接运算 ab 的构造

      

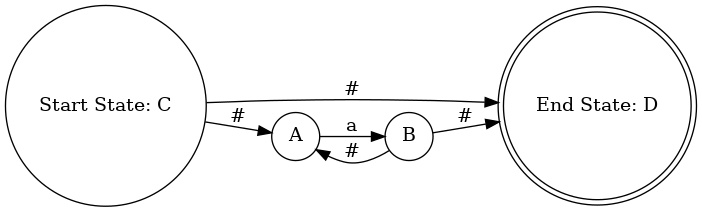
   3. Kleene 闭包 a* 的构造

      

   4. 分组运算 (ab)|c 的构造

      

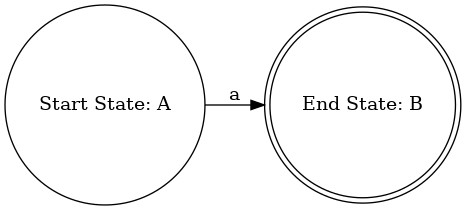
（3）输出 NFA，生成 dot 文件

graphviz (Graph Visualization Software) 是一个由 AT&T 实验室启动的开源工具包，用于绘制 DOT 语言脚本描述的图形。

​ DOT 语言语法规则：

1. 设置图形为有向图，并写入一个左花括号，表示图的开始；
2. 设置布局为横向布局；
3. 设置节点形状为圆形，NFA 的结束状态的节点的形状是双圆形；
4. 写入 NFA 的状态和转移的信息，如：添加起始状态和结束状态的标签 “Start State” 和 “End State”，根据 NFA 的边集，添加状态之间的转移边及对应的转移标签 tranSymbol；
5. 向文件中写入了一个右花括号，表示图的结束。
6. 最后，通过命令：dot -Tpng nfa_graph.dot -o nfa.png 可以将生成的 DOT 文件用 DOT 渲染工具（Graphviz）进行可视化。

​ 具体代码如下：

//生成NFAdot文件
void generateDotFile_NFA(const elem& nfa) {
	std::ofstream dotFile("nfa_graph.dot");

	if (dotFile.is_open()) {
		dotFile << "digraph NFA {\n";
		dotFile << "  rankdir=LR;  // 横向布局\n\n";
		dotFile << " node [shape = circle];   // 状态节点\n\n";

		dotFile << nfa.endName.nodeName << " [shape=doublecircle];\n";
		// 添加 NFA 状态
		dotFile << "  " << nfa.startName.nodeName << " [label=\"Start State: " << nfa.startName.nodeName << "\"];\n";
		dotFile << "  " << nfa.endName.nodeName << " [label=\"End State: " << nfa.endName.nodeName << "\"];\n";

		// 添加 NFA 转移
		for (int i = 0; i < nfa.edgeCount; i++) {
			const edge& currentEdge = nfa.edgeSet[i];
			dotFile << "  " << currentEdge.startName.nodeName << " -> " << currentEdge.endName.nodeName << " [label=\"" << currentEdge.tranSymbol << "\"];\n";
		}

		dotFile << "}\n";

		dotFile.close();
		std::cout << "NFA DOT file generated successfully.\n";
	}
	else {
		std::cerr << "Unable to open NFA DOT file.\n";
	}
}

（4）通过子集构造法将 NFA 转换为 DFA，并生成 dot 文件

​ 子集构造法：将 NFA 的状态集合分成若干个子集，每个子集代表一个 DFA 的状态。子集之间的转移关系，由 NFA 中的转移关系和空转移决定。具体步骤如下：

1. 计算 NFA 的初始状态的 ε 闭包，即包含初始状态和所有通过空转移可以到达的状态的集合。将这个集合作为 DFA 的初始状态，并标记为未处理。
2. 从未处理的状态集合中选取一个状态（一般是按照顺序），对于每个输入符号，计算该状态经过该符号可以到达的 NFA 状态的集合，再计算这个集合的 ε 闭包，得到一个新的状态集合。如果这个集合是新出现的，就将其标记为未处理，否则就是已处理的。根据这个过程，建立 DFA 的转移关系。
3. 重复第 2 步，直到没有未处理的状态集合为止。此时，DFA 的状态集合和转移关系就构造完成了。
4. 确定 DFA 的终止状态，即包含 NFA 的终止状态的状态集合。

​ 同 NFA，对 DFA 进行可视化：

//生成DFA的dot文件
void generateDotFile_DFA(vector<DFAState>& dfaStates, vector<DFATransition>& dfaTransitions) {
	std::ofstream dotFile("dfa_graph.dot");

	if (dotFile.is_open()) {
		dotFile << "digraph DFA {\n";
		dotFile << "  rankdir=LR;  // 横向布局\n\n";
		dotFile << " node [shape = circle];   // 初始状态\n\n";
		dotFile << dfaStates.back().stateName << "[shape = doublecircle];\n";
		// 添加DFA状态
		for (const auto& state : dfaStates) {
			dotFile << "  " << state.stateName;
			dotFile << " [label=\"State " << state.stateName;
			if (state.stateName == dfaStates.front().stateName) dotFile << "\\n(startState)";
			if (state.stateName == dfaStates.back().stateName) { 
				dotFile << "\\n(endState)"; 
			}
			dotFile << "\"];\n";
		}
		dotFile << "\n";

		// 添加DFA转移
		for (const auto& transition : dfaTransitions) {
			dotFile <<"  " <<transition.fromState.stateName << " -> " << transition.toState.stateName << " [label=\"" << transition.transitionSymbol << "\"];\n";
		}

		dotFile << "}\n";

		dotFile.close();
		std::cout << "DFA DOT file generated successfully.\n";
	}
	else {
		std::cerr << "Unable to open DOT file.\n";
	}
}

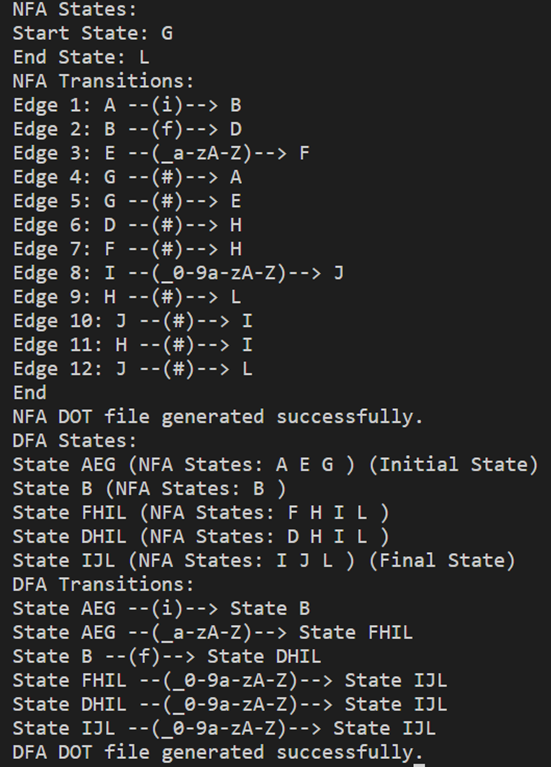
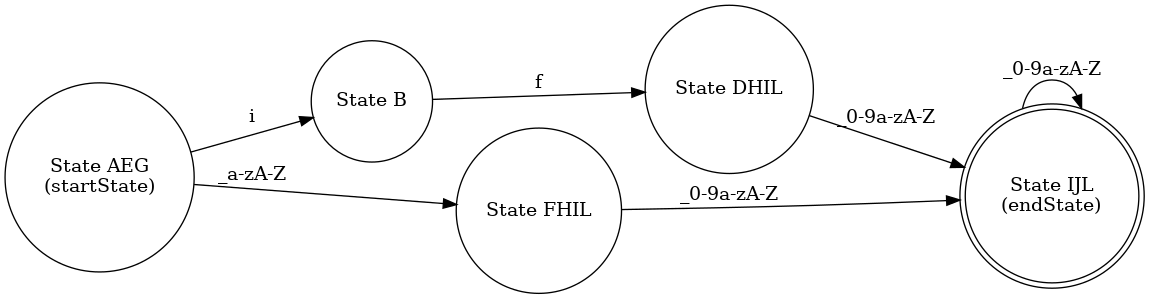
​ 测试案例：正则表达式：(if)|[_a-zA-Z][_0-9a-zA-Z]*

​ 输出：

• dot -Tpng nfa_graph.dot -o nfa.png 可视化 NFA

  

• dot -Tpng dfa_graph.dot -o dfa.png 可视化 DFA