索引调优

PJ——索引调优

1、任务要求

• 阅读材料：J. M. Hellerstein, J. F. Naughton, A. Pfeffer. Generalized Search Trees for Database Systems. In VLDB 1995.

• 背景描述：GiST 的意思是通用的搜索树（Generalized Search Tree），它是一种平衡树结构的访问方法，在系统中作为一个基本模版，可以使用它实现任意索引模式。B-trees、R-trees和许多其它的索引模式都可以用 GiST 实现。

• 作业要求：

  1. 阅读材料的简要阅读报告 (pdf)

  2. 索引实践报告（二选一）

     1. 对PG代码中的Gist使用性能进行分析，并形成报告 (pdf)
        • PG支持快速造数据，数据量建议百万条及以上
        • 主要为 Gist，B-trees，R-trees，RD-trees之间的性能比较分析，参考「参考材料2」
     2. 用PG中的Gist实现一类索引，并形成报告 (pdf, source codes)
        • 可选索引：B+trees，Hash，倒排索引
        • 实现规范参见「参考材料3」
        • 源码组织类似「参考材料4」即可，包含测试和README

  3. README，标明小组人员及分工表

  • 以上所有文件压缩在一个zip文件内，文件名「姓名1_学号1，姓名2 _学号2….zip」
  • 推荐使用PostgreSQL 14.x Linux

• 参考材料

  1. PostgreSQL: Documentation: 14: F.7. btree_gist
  2. PostgreSQL索引(5) – GiST – PostgreSQL数据库内核探究 (mengqingzhong.com)
  3. PostgreSQL: Documentation: 14: 65.3. Extensibility
  4. jinyyu/tlsh_gist (github.com)

• 附加说明

  • 小组/个人作业，每组提交一份文件，每组成员得分相同

  • 四个作业之一，取已做作业中的最高分作为作业得分

  • 本次作业结束后可换组

2、材料阅读报告

1. Introduction

1、实现搜索树扩展的两种主要思路

1. $Specialized\space Search\space Tree$：为解决特定的问题实现专用的搜索树。问题：实现和维护搜索树的工作量巨大；随着新应用产生，需要重新开发一种搜索树
2. $Search\space Trees\space For\space Extensible\space Data\space Types$：为避免开发新的搜索树类型，扩展其支持的数据类型。问题：虽然扩展了支持的数据类型，但是并没有扩展搜索树上可支持的查询的种类，依然只能支持相等或者范围查询（不灵活）

2、Gist 优点

1. 在支持的数据类型和查询种类方面都很容易扩展（可扩展性）
2. 可以实现基于同一个代码库实现不同的索引，支持不同的应用（统一性）
3. 很容易配置，为了实现不同用途的搜索树，只需要在数据库中注册 $6$ 种方法（易配置）

3、Gist 存在的问题

• $Gist$ 产生的搜索树并不总是可以有效地支持查询，何时以何种方式在一些非标准化的问题上构建一棵高效的查询树，仍需要进一步通过试验进行探索。

4、文章结构

• 第 $2$ 节：说明并概括了数据库搜索树的基本特性

• 第 $3$ 节：介绍了广义搜索树对象及其结构、属性和行为

• 第 $4$ 节：提供了三种不同类型的搜索树的 $GiST$ 实现

• 第 $5$ 节：介绍了一些性能结果，探讨了构建有效搜索树所涉及的问题

• 第 $6$ 节：检查了在成熟的 $DBMS$ 中实现 $GiST$ 时需要考虑的一些细节

• 第 $7$ 节：最后总结了这项工作的重要性，以及未来的研究方向

2. The Gist of Database Search Trees

1、搜索树介绍

• 简单示意图如下：

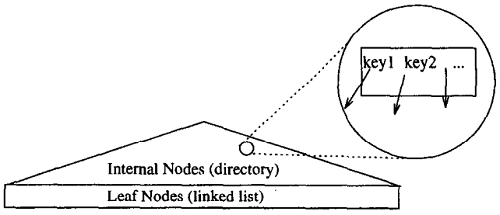
• 搜索原理：每个内部节点都包含一系列 $key$ 和 $pointer$。要搜索与查询谓词 $q$ 匹配的元组，需要从根节点开始查找。对于节点上的每个指针，如果关联的 $key$ 与 $q$ 一致，即 $key $不排除指针下方存储的数据可能匹配 $q$ 的可能性，则遍历指针下方的子树，直到找到所有匹配的数据。

• $key$ 的唯一限制：必须在逻辑上匹配存储在它下面的每一个数据，以便一致性检查不会遗漏任何有效数据。在 B+tree 和 R-tree 中，$key$ 的本质是一个 “包含” 谓词：它描述了一个连续的区域，其中包含 $pointer$ 下的所有数据。但是，“包含” 谓词并不是唯一可能出现的关系。就像在 R-tree 中，节点上的 $key$ 可能出现 “重叠” 这样的关系，即一个节点上的两个 $key$ 下面可能保存着某些相同的元组。

2、Gist 设计思路

• $key$ 的设计：搜索关键字 $key$ 是可以对其下的每一个数据都成立的任意谓词。如果给定这样一个灵活的数据结构，用户可以通过将数据组织成任意嵌套的子类别来自由地形成树，每一个都可以用一些特殊的谓词来标记。反过来，抓住数据库搜索树的本质：它是数据集分区的层次结构，每一个分区都有一个分类，用以保存分区中的所有数据，可以基于分类进行任意谓词的搜索。

• 谓词 $q$ 的设计：为了支持对给定谓词 $q$ 的搜索，用户必须提供一个返回布尔类型的方法来判断 $q$ 是否与给定的 $key$ 一致，搜索通过遍历与 $key$ 关联的指针来进行。当节点数据过多或者占用空间过大时，通过用户提供的分裂算法来控制数据的分组，并且可以使用用户提供的 $key$ 完成对分组的表征。因此，通过向用户公开关键方法和拆分方法，可以构建任意的搜索树，支持可扩展的查询集。

3. The Generalized Search Tree

3.1 structure

​ $Gist$ 是一颗平衡树，它的每个节点的扇出在 $kM$ 和 $M$ 之间，其中 $\frac{2}{M}\leqslant k\leqslant \frac{1}{2}$，根节点的扇出可以在 $2$ 和 $M$ 之间。其中常数 k 被称为最小填充因子，叶子节点包含 $(p,\space ptr)$ 这样的键值对，其中 $p$ 是被用作搜索关键字的谓词，而 $ptr$ 是数据库中某个元组的标识符。非叶子节点包含 $(p,\space ptr)$ 这样的键值对，其中 $p$ 是被用作搜索关键字的谓词，而 $ptr$ 是指向另一个节点的指针

​ 谓词可以包含任意数量的自由变量，只要树的叶子节点引用的任意单个元组能够装下，为了方便说明，这里假设树中的各项占用空间大小是一样的，可变大小的项在第 $6$ 节介绍。假设给定项 $E=(p,\space ptr)$ 的实现中，可以访问 $E$ 当前所在的节点

3.2 Properties

以下属性在 $Gist$ 中是固定的：

1. 除了根节点外每个节点包含 $kM$ 到 $M$ 个索引项
2. 每个叶节点中的索引项 $(p,\space ptr)$ 在用指定的元组实例化时，$p$ 为 $true$（即 $p$ 对元组成立）
3. 每个非叶子节点中的索引项 $(p,\space ptr)$，当使用从 $ptr$ 可达的任意元组对其实例化时，$p$ 为 $true$。和 $R-tree$ 不同的是：对于某个从
   $ptr$ 可达的索引项 $(p’,\space ptr’)$，不要求 $p’\rightarrow p$，只要 $p$ 和 $p’$ 都适用于从 $ptr’$ 可达的元组
4. 根节点至少有两个子节点，除非它本身也是叶子节点
5. 所有叶子节点出现在同一层

3.3 Key Method

​ 原则上，$Gist$ 中的 $key$ 可以是任意的谓词。实际使用中，$key$ 来自用户定义的对象，同时提供 $Gist$ 需要的一些方法的实现。例如， B+tree 中 $key$ 是数字类型，标识数据的范围；R-tree 中 $key$ 的类型是外接矩阵，标识区域等等。

​ 以下 $6$ 个关键的方法，是预定义的需要用户实现的方法：

1. $\mathbf{Consistent}(E,q)$：给定一个索引项 $E=(p,\space ptr)$ 以及一个查询谓词 $q$，如果 $p\wedge q$ 一定不满足，返回 $false$，否则返回 $true$。==注意==：这里不需要精确查找，$\mathbf{Consistent}$ 有可能产生误报，会导致不必要的子树的查询，从而影响性能，但算法正确性不受影响。
2. $\mathbf{Union}(P)$：给定一个索引项的集合 $P$，包含索引项 $(p_1,ptr_1),…,(p_n,ptr_n)$，可以通过 $(p_1\vee p_2\vee … p_n)\rightarrow r$ 的形式返回谓词 $r$，$r$ 包含 $ptr_1$ 到 $ptr_n$ 所有的元组
3. $\mathbf{Compress}(E)$：给定索引项 $E=(p,\space ptr)$，返回索引项 $(\pi,ptr)$，其中 $\pi$ 是 $p$ 的压缩表示
4. $\mathbf{Decompress}(E)$：给定一个压缩后的索引项 $E=(\pi,\space ptr)$，其中，$\pi=\mathbf{Compress}(p)$，返回一个索引项 $(r,ptr)$，满足 $p\rightarrow r$。==注意==：这可能是一种有损的压缩，因为不需要满足 $p\leftrightarrow r$
5. $\mathbf{Penalty}(E_1,E_2)$：给定两个索引项 $E_1=(p_1,\space ptr_1)$，$E_2=(p_2,\space ptr_2)$，返回一个将 $E_2$ 插入以 $E_1$ 为根的子树的代价。该方法用于辅助插入和分裂算法
6. $\mathbf{PickSplit}(P)$：给定一个包含 $M+1$ 个索引项的节点 $P$，将 $P$ 分裂为两个集合 $P_1$ 和 $P_2$，每一个至少包含 $kM$ 个索引项，通常希望以一种最优的方式进行拆分，但最终取决于用户

3.4 Tree Methods

​ 上一小节提到的方法需要开发者提供，本小节的方法是由 $Gist$ 提供，==注意==：$keys$ 在节点上是压缩的，从节点读取时需要解压缩，后续不在赘述。

1. Search

Algorithm Search(R, q)

Input: GiST rooted at R, predicate q 

Output: all tuples that satisfy q 

Sketch: Recursively descend all paths in tree whose keys are consistent with q. 

S1: [Search subtrees] If R is not a leaf, check each entry E on R to determine whether Consistent(E, q). For all entries that are Consistent, invoke Search on the subtree whose root node is referenced by E.ptr.

S2: [Search leaf node] If R is a leaf, check each entry E on R to determine whether Consistent(E, q). If E is Consistent, it is a qualifying entry. At this point E.ptr could be fetched to check q accurately, or this check could be left to the calling process.

​ ==注意==：查询谓词 $q$ 可以是精确匹配（相等）谓词，也可以是同时有多个值满足的谓词。后者包括 ”range“ 或 window“ 谓词，如在 B+tree 或 R-tree 中，还有不基于连续区域的谓词（例如集合中的包含谓词）

2. Search In Linearly Ordered Domains

​ 如果被索引的数据线性有序，且查询通常是相等或者范围这样的谓词，那么本小节中定义的 $FindMin$ 和 $Next$ 方法可以实现更高效地搜索。要使此选项可用，用户需要在创建搜索树的时候执行一些额外的步骤：

• $\mathbf{IsOrdered}$ 是在创建树的时候设置的一个静态属性，默认值是 false；需要设置为 true
• $\mathbf{Compare}(E_1,E_2)$ 需要被注册，给定两个索引项 $E_1=(p_1,\space ptr_1)$ 和 $E_2=(p_2,\space ptr_2)$，$\mathbf{Compare}$ 方法返回 $p_1$ 是否在 $p_2$ 之前，或者 $p_1$ 在 $p_2$ 之后，或者 $p_1$ 和 $p_2$ 相等。$\mathbf{Compare}$ 用于在每个节点内插入数据
• $\mathbf{PickSplit}$ 方法必须保证 $P$ 分裂为 $P_1$ 和 $P_2$ 节点后，对于任意 $P_1$ 上的索引项 $E_1$、$P_2$ 上的索引项 $E_2$，$\mathbf{Compare}(E_1,E_2)$ 返回 $E_1$ 在 $E_2$
• 保证一个节点内没有两个重叠的 $key$，即一个节点内的任意 $E_1$ 和 $E_2$，$\mathbf{Consistent}(E_1,E_2.p)=false$

​ 如果执行了上面 $4$ 个步骤，则可以通过调用 $FindMin$ 并重复调用 $Next$ 来处理相等和范围查询。而其他类型的谓词仍然可以通过通用的搜索方法来处理，$FindMin/Next$ 比使用 $Serach$ 遍历更高效，因为 $FindMin$ 和 $Next$ 只沿着一个根到叶子的路径访问非叶子节点

Algorithm FindMin(R, q) 

Input: GiST rooted at R, predicate q 

Output: minimum tuple in linear order that satisfies q 

Sketch: descend leftmost branch of tree whose keys are Consistent with q. When a leaf node is reached, return the first key that is Consistent with q. 

FM1: [Search subtrees] If R is not a leaf, find the first entry E in order such that Consistent(E, q) . If such an E can be found, invoke FindMin on the subtree whose root node is referenced by E :ptr. If no such entry is found, return NULL. 

FM2: [Search leaf node] If R is a leaf, find the first entry E on R such that Consistent(E, q), and return E. If no such entry exists, return NULL.

​ 给定一个满足谓词 $q$ 的索引项 $E$，$Next$ 方法返回下一个满足 $q$ 的索引项，如果不存在则返回 $NULL$。如果是为了查找 $Next$ 只会在叶子节点上被调用

Algorithm Next(R, q, E) 

Input: GiST rooted at R, predicate q, current entry E 

Output: next entry in linear order that satisfies q 

Sketch: return next entry on the same level of the tree if it satisfies q. Else return NULL. 

N1: [next on node] If E is not the rightmost entry on its node, and N is the next entry to the right of E in order, and Consistent(N, q), then return N. If :Consistent(N, q), return NULL. 

N2: [next on neighboring node] If E is the righmost entry on its node, let P be the next node to the right of R on the same level of the tree (this can be found via tree traversal, or via sideways pointers in the tree, when available [LY81].) If P is non-existent, return NULL. Otherwise, let N be the leftmost entry on P . If Consistent(N, q), then return N, else return NULL.

3. Insert

​ 插入流程保证 $Gist$ 的平衡，它与 R-tree 的插入非常相似，它是 B+tree 更简单的插入流程的泛化。插入允许指定插入 $level$，这允许后续方法使用 Insert 从树的内部节点重新插入数据。假设叶子节点是 $0$ 层，层号从叶子节点向上不断增加，新插入的项目出现在 $level=0$ 层

Algorithm Insert(R, E, l) 

Input: GiST rooted at R, entry E = (p, ptr), and level l, where p is a predicate such that p holds for all tuples reachable from ptr. 

Output: new GiST resulting from insert of E at level l. 

Sketch: find where E should go, and add it there, splitting if necessary to make room. 

I1. [invoke ChooseSubtree to find where E should go] Let L = ChooseSubtree(R, E, l) 

I2. If there is room for E on L, install E on L (in order according to Compare, if IsOrdered.) Otherwise invoke Split(R, L, E). 

I3. [propagate changes upward] AdjustKeys(R, L).

​ ChooseSubtree 可用于在树的任何 $level$ 找到插入的最佳节点。当 IsOrdered 属性是 true 时，必须仔细编写 Penalty 方法以确保 ChooseSubtree 按顺序到达正确的叶子节点。

Algorithm ChooseSubtree(R, E, l) 

Input: subtree rooted at R, entry E = (p, ptr), level l 

Output: node at level l best suited to hold entry with characteristic predicate E.p 

Sketch: Recursively descend tree minimizing Penalty 

CS1. If R is at level l, return R; 

CS2. Else among all entries F = (q, ptr') on R find the one such that Penalty(F, E) is minimal. Return ChooseSubtree(F.ptr', E, l).

​ split 算法利用用户自定义的 PickSplit 方法来决定如何拆分节点，包括处理正在进行插入的新元组。一旦数据分成两份，Split 就会为其中一份生成新的节点，将其插入树中，并更新树中新节点之上的 $key$

Algorithm Split(R, N, E) 

Input: GiST R with node N, and a new entry E = (p, ptr). 

Output: the GiST with N split in two and E inserted. 

Sketch: split keys of N along with E into two groups according to PickSplit. Put one group onto a new node, and Insert the new node into the parent of N. 

SP1: Invoke PickSplit on the union of the elements of N and fEg, put one of the two partitions on node N, and put the remaining partition on a new node N0 . 

SP2: [Insert entry for N0 in parent] Let EN' = (q, ptr'), where q is the Union of all entries on N', and ptr' is a pointer to N'. If there is room for EN' on Parent(N), install EN' on Parent(N) (in order if IsOrdered.) Otherwise invoke Split(R, Parent(N), EN').

SP3: Modify the entry F which points to N, so that F.p is the Union of all entries on N.

​ 步骤 SP3 修改父节点信息，以显示节点 $N$ 的修改。 这些修改通过插入流程中的步骤 I3 向上传播到树中的其他部分，同时传播了由于插入 $N’$ 引起的树结构的变化。

​ AdjustKeys 方法确保一组谓词之上的 key 适用于下面的所有元组

Algorithm AdjustKeys(R, N) 

Input: GiST rooted at R, tree node N 

Output: the GiST with ancestors of N containing correct and specific keys 

Sketch: ascend parents from N in the tree, making the predicates be accurate characterizations of the subtrees. Stop after root, or when a predicate is found that is already accurate.

PR1: If N is the root, or the entry which points to N has an already-accurate representation of the Union of the entries on N, then return. 

PR2: Otherwise, modify the entry E which points to N so that E.p is the Union of all entries on N. Then AdjustKeys(R, Parent(N).)

​ ==注意==：当 $\mathbf{IsOrdered}=true$ 时，AdjustKeys 通常不执行任何工作，因为这种情况下，节点上的谓词通常将数据分为几个范围，不需因为简单的插入或者删除而进行修改，AdjustKeys 会在步骤 PR1 中检测到这种情况，从而避免在树中的更高的 $level$ 调用 AdjustKeys，这种情况下，如果有需要可以完全绕过 AdjustKeys、

4. Delete

​ 删除算法保持树的平衡，同时尽可能保持树中 $key$ 的信息。当树中的 $key$ 存在线性顺序时，使用 B+tree 风格的 ”$borrow\space or\space coalesc$“ 技术。否则，使用 R-tree 风格的重新插入技术。篇幅原因，文中省略删除算法

4. The Gist for Three Applications

这一章的内容是给出了三个基于 $Gist$ 实现的具体的索引类型，包括 B+tree、R-tree 和 RD-tree，其中主要描述了实现这几种索引类型时，$Gist$ 定义的需要用户实现的接口是如何实现的。

4.1 GiSTs Over $\mathbb{Z}$ (B+trees)

4.2 GiSTs Over Polygons in $\mathbb{R}$ (R-trees)

4.3 GiSTs Over $\mathcal{P}(\mathbb{Z})$ (RD-trees)

5. Gist Performance Issues

1. 无重叠 $key$

• 对于没有重叠 $key$ 的平衡树（如 B+tree）需要检查的最大节点数（I/O 次数）很容易检验：对于无重叠数据的 $point\space query$，查询次数是树的高度。对于一个 $n$ 个元组的数据库而言是 $O(log\space n)$，这个上限不能保证。
• 但是，对于有重叠 $key$ 的树而言，相同的数据可能出现在不同的节点上，这会导致对树中的多条路径进行查询。Gist 的性能随着节点上出现重叠 $key$ 的情况而变化。

2. 有重叠 $key$

1、主要原因

• 数据重叠和 $key$ 压缩带来的信息损失

  • 数据重叠：如果树中的数据出现重叠，那么 $key$ 很可能也出现重叠。例如数据集中的数据完全相同，这种情况下会生成低效的索引，利用顺序扫描可能更合适

  • 压缩带来的信息损失：即使两个原始数据可能不重叠，但如果 $Compress/Decompress$ 方法不能产生精确的 $key$，那么可能导致数据重叠。例如 R-tree，$Compress$ 方法生成外接矩形，如果源数据不是矩形的，那么可能导致数据有损

2、性能的影响

​ 上述两个因素对性能的影响如下图所示，初始时没有数据重叠或者压缩导致精度丢失的问题，此时具有最佳的性能。随着数据重叠的增加或压缩导致的精度问题出现，性能开始下降。最坏情况下任意的查询语句都会命中所有的 $key$，这种情况下需要遍历整棵树

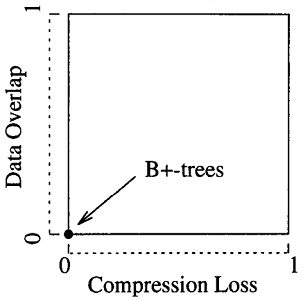
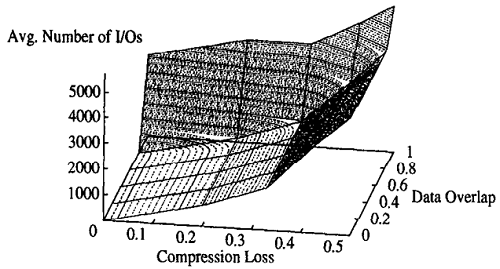
3、模型验证

​ 选择 RD-trees 来验证性能（I/O 次数）在上图参数空间中的变化：

6. Implementation Issues

总结实现 $Gist$ 需要考虑的问题：

• In-memory Efficiency：上一小节讨论了 $Gist$ 如何提升磁盘访问方面的效率，为简化内存管理方面的开销，将 $node$ 对象的实现开放为可扩展的。例如，可以重载线性排序的 $Gist$ 的 $node$ 实现，以支持二分查找；可以重载支持 hB-tree 的 $node$ 实现，以支持 hB-tree 所需的专用内部结构

• Concurrencu-control, Recovery and Consistency：高并发、可恢复性、一致性是数据库的关键

• Variable-Length Keys：通常允许变长 $key$ 是一个非常有用的特性，特别是 $Gist$ 中允许使用压缩算法。但是这需要在实现树操作方法时尤其小心，例如 Insert 和 Split

• Bulk Loading：在无序的数据上，如何在一个大的已经存在的数据集上有效构建索引，当前仍不清晰。应该为 $Gist$ 扩展 Bulk Load 方法，来实现不同类型的数据集的批量加载

• Optimizer Integration：要将 $Gist$ 和查询优化器集成，必须让优化器知道哪些查询谓词与哪些 $Gist$ 是匹配的。而估算 $Gist$ 的代价更困难，需要进一步研究

• Coding Detail：两种建议实现 $Gist$ 的方式：

  • $Extensible\space GiST$：像 $POSTGRES$ 或者 $Illustra$ 一样，在运行时可扩展，这样可以非常方便使用；
  • $Template\space GiST$：像 $SHORE$ 一样，在编译时可扩展，这样可以更高效。

  以上两种方式基于相同的代码库构建，不需要复制逻辑

7. Summary and Future Work

• Gist 对搜索树进行了抽象，提取了它们的一些共同特征，对各种搜索树进行了结构上的统一

• Gist 具有非常好的扩展性，允许对任意的数据集进行索引和查询，这引出了何时以何种方式生成搜索树的问题

• Gist 的可扩展性引发的研究问题：

  • 可索引性（$Indexability$）：$Gist$ 虽然提供了一种为任意类型建立索引的方法，但是对于 ”可索引性“ 还缺乏理论来描述：对于一个给定的数据集，针对给定的查询是否能够使用索引
  • 索引非标准数据（$Indexing Non-Standard Domains$）：实际上，对一些非标准数据，例如集合、图形、序列、图片、音频、视频等，探索这些数据类型，会对理论探索提供一些有趣的反馈。对集合数据的 RD-tree 的研究已经开始：已经在 $SHORE$ 和 $Illustra$ 中实现了 RD-tree，只是用的时 R-tree 而不是 $Gist$。一旦从 R-tree 转到 $Gist$ 上，也可以通过实现新的 $PickSplit$ 方法和新的谓词实现这一点
  • 查询优化和代价评估（$Query\space Optimization\space and\space Cost\space Estimation$）：需要考虑搜索 $Gist$ 的代价，当前代价评估对 B+ tree 而言时准确且合理的，对 R-tree 而言可能相对差一些。R-tree 上的代价评估已经有一些工作已经完成，但是对更通用的 Gist 而言还有很多工作要做。另外，需要由用户实现的接口可能是非常耗时的操作，这些方法的 CPU cost 要注册给优化器。然后优化器在做代价评估时，将这些 CPU cost 正确地纳入计算中
  • 有损 $key$ 压缩技术（$Lossy\space Key\space Compression\space Technique$）：随着新的数据类型被索引，可能有必要找到新的有损压缩算法，来保留 Gist 的属性
  • 算法提升（$Algorithmic\space Improvement$）：$Gist$ 的插入算法基于 R-tree 的插入算法。R-tree 使用了某种修改过的算法，对于空间数据似乎有一些性能的提升。特别是，R-tree 在分裂期间 ”强制重新插入“ 能获得很好的收益。如果这些技术证明是有益的，它们会被纳入到 Gist 中，作为可选项或者默认选项。要统一 R-tree 和 R-tree 中的并发控制和恢复方面的内容修改还需要一些工作

3、Gist 索引性能分析报告

一、性能指标

1. SQL 处理过程

• 查询编译
  • 查询分析：由 SQL 查询语句生成查询树
  • 查询重写：对查询树重写并生成新的查询树，以提供对规则和视图的支持
  • 查询优化
    • 生成路径：由查询树计算最优路径
    • 生成计划：根据最优路径，生成执行计划和执行树。
• 查询执行
  • 执行计划：执行执行树的每个 node，最终返回结果给用户 terminal
  • 调度：将请求分配到合适的处理模块
  • 附件命令处理：处理建表、备份等命令

2. 计划树分析

2.1 EXPLAIN 工具

​ EXPLAIN 命令：可以查看规划器生成的查询计划。查询计划的结构是一个计划结点的树，EXPLAIN 给计划树中每个结点都输出一行，显示基本的结点类型和计划器为该计划结点的执行所做的开销估计。第一行（最上层的结点）是对该计划的总执行开销的估计，一个上层结点的开销包括它的所有子结点的开销。

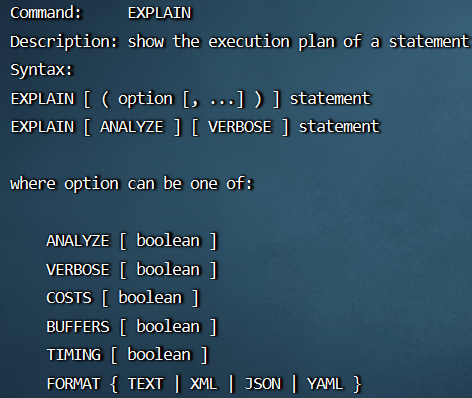
• ANALYZE，执行命令并且显示实际的运行时间和其他统计信息，这个参数默认被设置为 FALSE

• VERBOSE，显示关于计划的额外信息。特别是：计划树中每个结点的输出列列表、模式限定的表和函数名、总是把表达式中的变量标上它们的范围表别名，以及总是打印统计信息被显示的每个触发器的名称，这个参数默认被设置为 FALSE

• COSTS，包括每一个计划结点的估计启动和总代价，以及估计的行数和每行的宽度，这个参数默认被设置为 TRUE

• BUFFERS，显示关于缓冲区（共享块、本地块、临时块读和写的块数）使用的信息，可用于识别查询的哪些部分是 I/O 密集程度最高的。该参数默认被设置为 FALSE 且只能和 ANALYZE 参数一起使用，

• TIMING，在输出中包括实际启动时间以及在每个结点中花掉的时间。只有当 ANALYZE 也被启用时，这个参数才能使用，它的默认被设置为 TRUE

• FORMAT，指定输出格式，可以是 TEXT、XML、JSON 或者 YAML。非文本输出包含和文本输出格式相同的信息，但是更容易被程序解析，这个参数默认被设置为 TEXT

2.2 EXPLAIN 结果说明

1. 执行类型

• 全表扫描|顺序扫描 (Seq Scan)：将表的所有数据块从头到尾读一遍，然后从数据块中找到符号条件的数据块
• 索引扫描 (Index Scan)：在索引中找到数据行的物理位置，然后再到表的数据块中把相应的数据读出来
• 位图扫描 (Bitmap Index Scan $\rightarrow$ Bitmap Heap Scan)：索引的一种方式，把满足条件的行或块在内存中建一个位图，扫描完索引后，再根据位图到表的数据文件把数据读取出来
• 条件过滤 (Filter)：一般时在 WHERE 上过滤条件
• 嵌套循环 (Nestloop Join)：内表被外表驱动，外表返回的每一行数据都要在内表中检索到匹配的行。注意：外表（驱动表）选择小的表，内表（被驱动表）的连接字段要有索引，否则性能会很慢
• Hash 连接 (Hash Join)：优化器用 $2$ 个表中较小的表，并利用连接键在内存中建立散列表，然后扫描较大的表并探测散列表，找出与散列表匹配的行
• 合并连接 (Merge Join)：如果源数据上有索引或结果已经排好序，在执行排序合并连接时不需要排序，此时合并连接的性能优于 Hash Join

2. cost 值

• 顺序扫描一个数据块，cost值定为 $1$
• 随机扫描一个数据块，cost值定为 $4$
• 处理一个数据行的 CPU，cost值为 $0.01$
• 处理一个索引行的 CPU，cost值为 $0.005$
• 每个操作符的 CPU，cost值为 $0.0025$

3. Buffers

• shared read=1，代表数据来自磁盘而并非缓存
• shared hit=1，说明数据已经在cache中

4. Time

• Planning Time，生成执行计划的时间
• Execution Time，执行计划的时间

5. 其他信息

• rows，表示返回多少行
• width，表示每行平均宽度
• actual time，实际花费的时间
• loops=1，循环的次数
• Output，输出的字段名

2.3 规划器的统计数据

​ 统计信息：每个表和索引中的记录总数以及每个表和索引占据的磁盘块数，这两个信息被保存在 pg_class 的 reltuples 和 relpages 字段中，可以使用如下语句检索这些信息。

select relname,relkind,reltuples,relpages from pg_class;

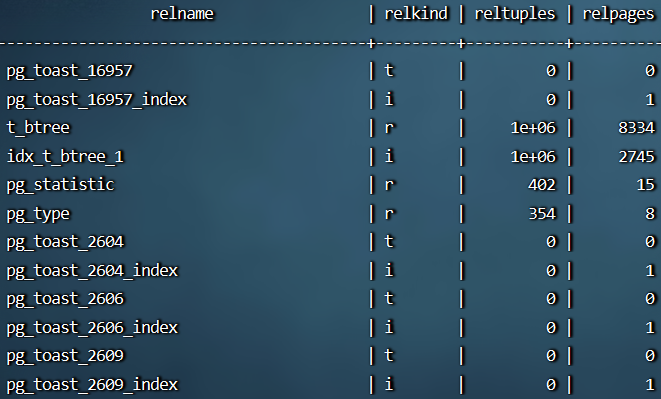
​ ==注意==：出于效率考虑，reltuples 和 relpages 不是实时更新的， 因此它们通常包含可能有些过时的数值。 它们被 VACUUM、ANALYZE和几个 DDL 命令更新，比如 CREATE INDEX。一个独立的 ANALYZE（没有和 VACUUM 在一起的） 生成一个 reltuples 的近似数值， 因为它并没有读取表里的每一行。规划器将把 pg_class 表里面的数值调整为和当前的物理表尺寸匹配，以此获取一个更接近的近似值。

3. 性能分析方法

• 首先，我们分析了一条 SQL 语句是如何工作的， 发现影响查询性能的关键是生成路径和生成计划两个模块

• 然后，我们查看 SQL 语句的执行计划并重点关注规划器如何使用统计信息

• 最后，从两个方面对 Gist 索引进行性能分析

  • 索引有效性：我们通过 EXPLAIN 命令获取 SQL 语句相关的统计信息，对比使用索引前后的执行时间来比较索引的有效性
  • 索引使用情况：查看索引使用的统计情况的表：pg_stat_user_indexes；使用命令：select * from pg_stat_all_indexes where relname = ‘t_btree’进行查看

二、PostgreSQL 索引

• PG 中提供的 $10$ 种索引：

1. B-tree 索引：适合所有的数据类型，支持可以排成某些顺序的数据的等式和范围查询
2. Hash 索引：只能处理简单的等式比较
3. GIN 索引：用于包含多个组件值的数据值（如数组）的 “反向索引“
4. Gist 索引：它是一种平衡树结构的访问方法，是可以实现许多不同索引方案的基本模板
5. SP-Gist 索引：类似 Gist，是一个通用的索引接口，但是 SP-Gist 使用了空间分区的方法，使得 SP-Gist 可以更好的支持非平衡数据结构，例如：quad-trees、k-d tree、radis tree
6. BRIN 索引：是块级索引，有别于 B-tree 等索引，BRIN 记录并不是以行号为单位记录索引明细，而是记录每个数据块或者每段连续的数据块的统计信息。因此BRIN索引空间占用特别的小，对数据写入、更新、删除的影响也很小
7. RUM 索引：是一个索引插件，由 Postgrespro 开源，适合全文检索，属于 GIN 的增强版本
8. Bloom 索引：是 PostgreSQL 基于 bloom filter 构造的一个索引接口，属于 lossy 索引，可以收敛结果集（排除绝对不满足条件的结果，剩余的结果里再挑选满足条件的结果），因此需要二次 check，bloom 支持任意列组合的等值查询
9. ZomboDB 索引：是 PostgreSQL 与 ElasticSearch 结合的一个索引接口，可以直接读写 ES，实现数据的透明搜索
10. BitMap 索引：是 Greenplum 的索引接口，类似 GIN 倒排，只是 BitMap 的 key 是列的值，value 是 BIT（每个BIT对应一行），而不是行号 list 或 tree

默认情况下，CREATE INDEX 命令创建的是 B-tree 索引

1. B-tree 索引

• 应用场景：适合所有的数据类型，支持排序，支持大于、小于、等于、大于或等于、小于或等于的搜索
• 运行 demo 测试 B-tree 索引对性能的提升：

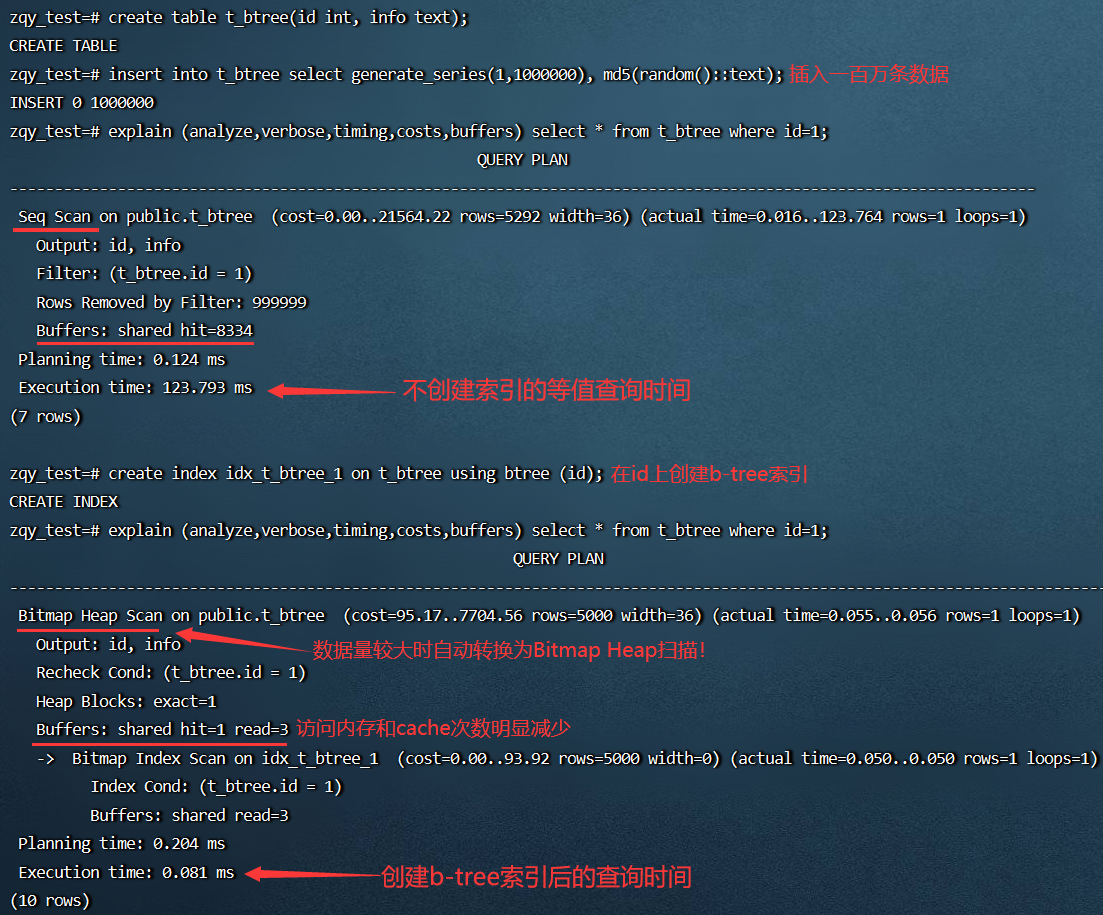
• ==问题==：我们在这里创建的索引类型是 B-tree，并不支持位图索引。而上图的执行计划中可以看到有个 “Bitmap Heap Scan”，为什么实际执行的却是基于位图索引的扫描？

  • PostgreSQL 开发者核心团队的成员 Tom Lane 给出的解释：

    A plain indexscan fetches one tuple-pointer at a time from the index, and immediately visits that tuple in the table. A bitmap scan fetches all the tuple-pointers from the index in one go, sorts them using an in-memory “bitmap” data structure, and then visits the table tuples in physical tuple-location order

    翻译：普通的索引扫描一次读一条索引项，而 BitMap Heap Scan 一次性将满足条件的索引项全部取出，并在内存中进行排序, 然后根据取出的索引项访问表数据。由于 BitMap Heap Scan 会输出整个数据块的数据，因此需要 recheck，对输出的索引项进行过滤

  • 其他解释：如果数据相关性较低，规划器认为，如果它执行普通的索引扫描，它将跳过整个表（物化视图）以获取所指示的行，从而导致大量随机 IO，这比顺序 IO 慢得多。通过执行位图扫描，它改进了这一点，因为位图本身就将索引中的行 “排序” 成它在表中找到它们的顺序，从而使表的读取更加顺序化。但位图扫描也并不总是有效。

  • 我们的理解：在读取数据量比较小时，index scan 比较合适；在读取数据量比较大的情况下，bitmap index scan 会更有优势，可减少随机读取，提升 I/O 效率

• 解决：由于我们后面要对比不同索引的性能，因此不希望系统自动优化使用位图索引扫描，通过 set enable_bitmapscan = off 禁用该优化器开关，从而来确保进行的是索引扫描

• 执行 B-tree 索引扫描的查询计划：

2. Gist 索引

应用场景：是一个通用的索引接口，可以使用 Gist 实现 B-tree、R-tree 等索引结构。不同的类型，支持的索引检索也各不一样：

1. 几何类型，支持位置搜索（包含、相交、在上下左右等），按距离排序
2. 范围类型，支持位置搜索（包含、相交、在左右等）
3. IP类型，支持位置搜索（包含、相交、在左右等）
4. 空间类型（PostGIS），支持位置搜索（包含、相交、在上下左右等），按距离排序
5. 标量类型，支持按距离排序

2.1 几何类型检索（R-tree）

2.2 标量类型排序（B-tree）

• 扩展 Gist 功能：因为 Gist 可以实现 B-tree 的索引结构，所以也可以在例如数字这种标量类型上使用 Gist 索引（虽然一般都不如B-tree索引效果好），这里需要使用 btree_gist 索引插件，它对 B-tree 固有的操作符增加了 Gist 功能

  

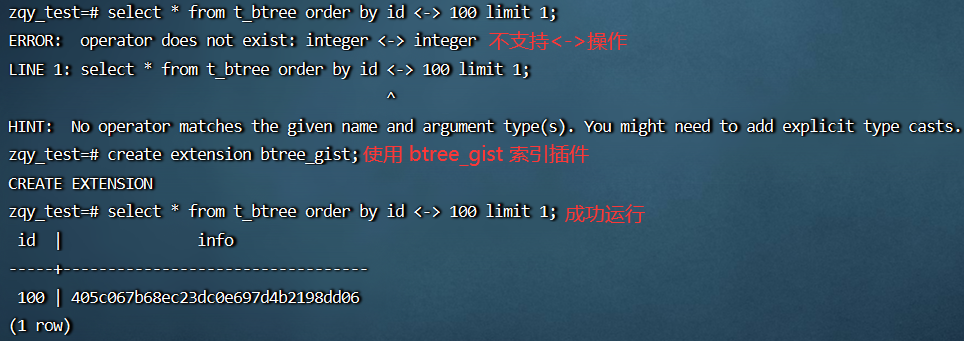
• 性能分析

  • 添加 Gist 索引前后性能对比

    • 使用索引前：
    
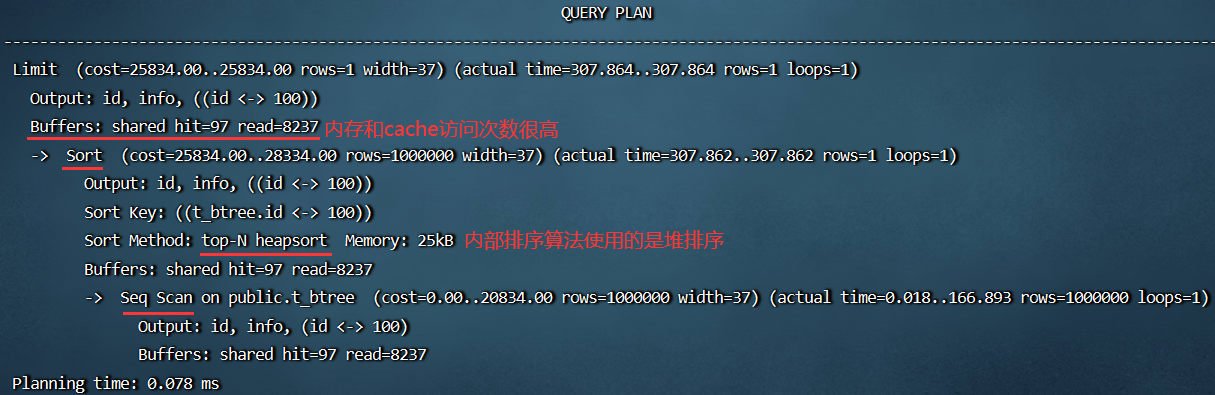
    • 使用索引后：
    

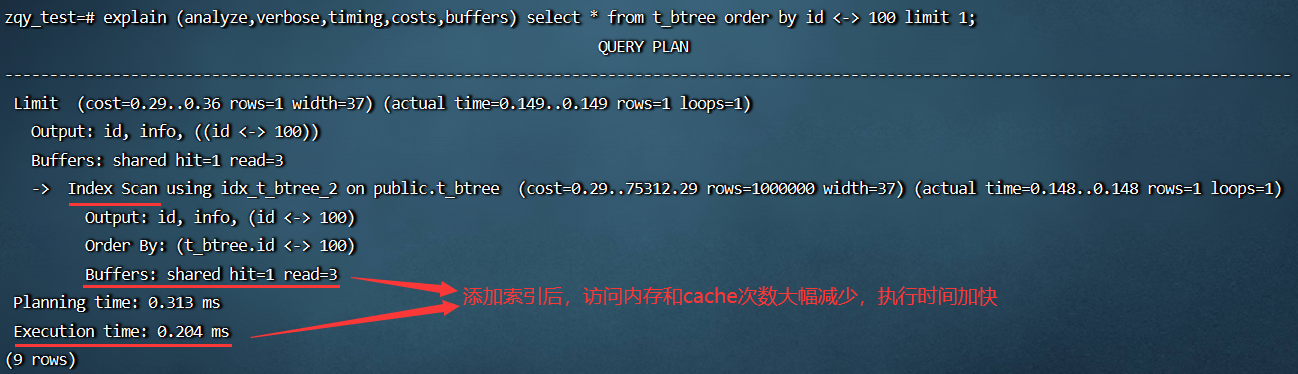
  • Gist 索引和 B-tree 索引对比

    • 性能对比
    

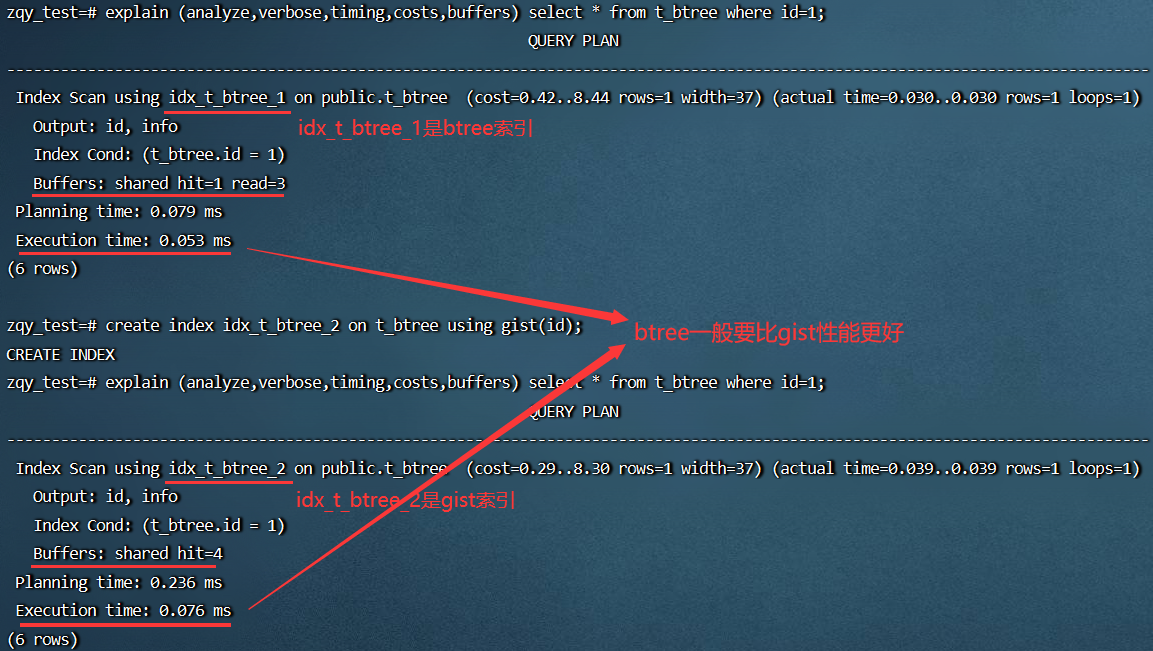
    • 占用空间对比

      

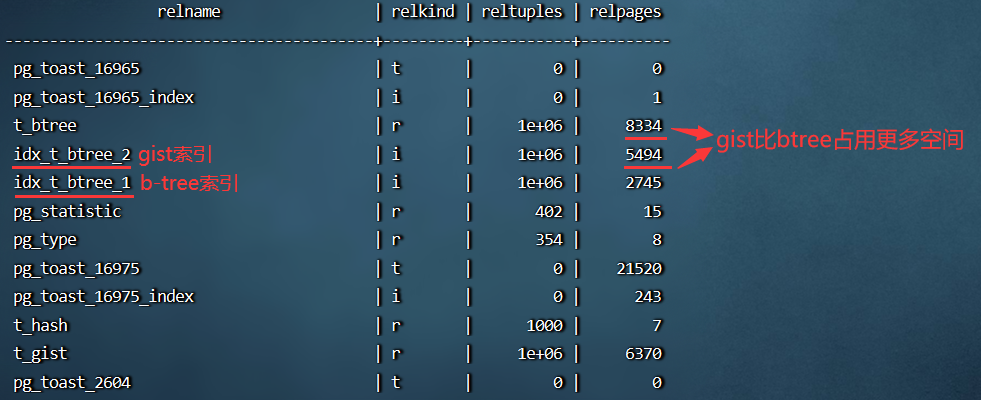
• 总结 Gist 和 B-tree 索引比较的优缺点：

  • 优点：和 B-tree 索引类似，同样适用于其他的数据类型。和 B-tree 索引相比，Gist 多字段索引在查询条件中包含索引字段的任何子集都会使用索引扫描，而 B-tree 索引只有查询条件包含第一个索引字段才会使用索引扫描
  • 缺点：Gist 索引性能上略差于 B-tree，且创建耗时较长，占用空间也比较大

2.3 全文检索（RD-tree）

• 全文检索：通过自然语言文档的集合来找到那些匹配一个查询的检索

• PostgreSQL 提供了两种数据类型用于支持全文检索：

  • tsvector：是一个无重复值的 lexemes 排序列表，即一些同一个词的不同变种的标准化

  • tsquery：存储用于检索的词汇，并且使用布尔操作符 &(AND)，|(OR) 和 !(NOT) 来组合它们，括号用来强调操作符的分组

  • 示意图：

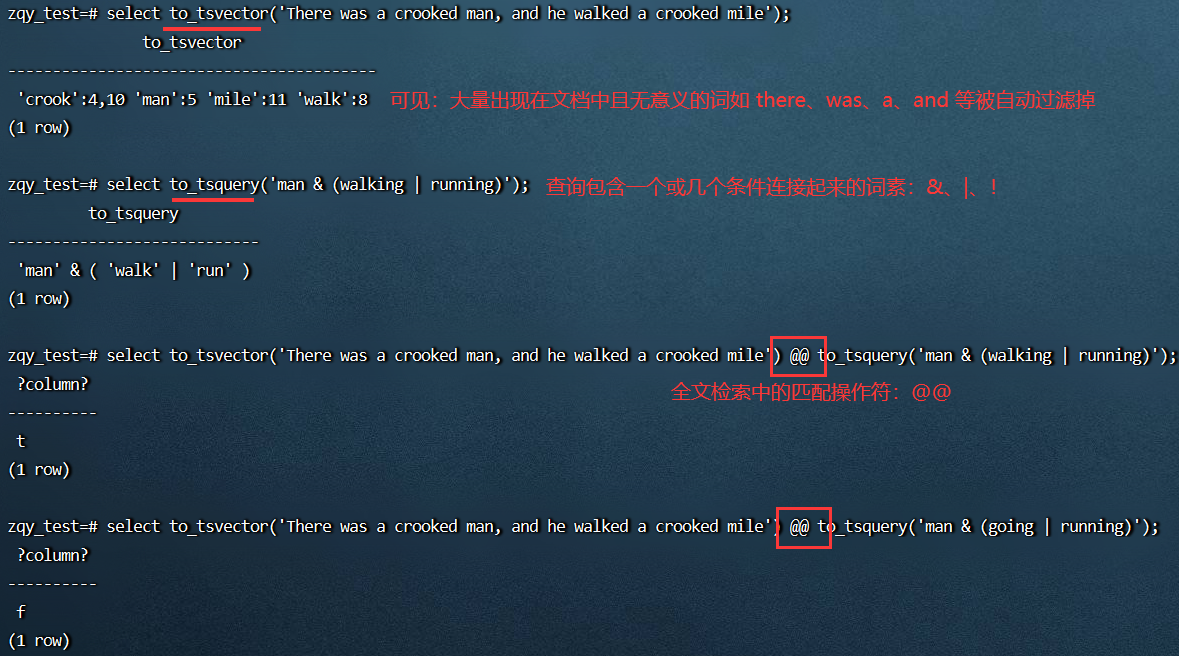
• 添加 Gist（RD-tree） 索引前后性能对比

三、Gist 性能对比实验

上一小节主要关注：PG 中 B-trees 索引和 Gist 索引的测试，以及添加索引后性能的提升

本小节主要进行：Gist，B-trees，R-trees，RD-trees 之间的性能比较分析

1. 实验设置

1.1 数据集准备

​ 我们的实验共分为三个部分：分别是对 Gist 实现的 B-tree、R-tree 以及 RD-tree 三种索引的性能对比分析。

​ 为了让实验结果更加可靠，我们分别为 B-tree、R-tree 索引各准备了 $4$ 个数据表，数据量分别为一百万条、两百万条、五百万条和一千万条；RD-tree 为 $3$ 个数据表，数据量分别为一百万条、两百万条、五百万条，用以观察不同数据量下各索引的性能变化以及性能瓶颈。各数据表的详细参数如下：

索引类型	数据量	数据类型	查询项
B-tree	1M，2M，5M，10M	id : integer，name : text	id
R-tree	1M，2M，5M，10M	id : integer，p : point	p
RD-tree	1M，2M，5M	id : integer，words : text，words_tsv : tsvector	words_tsv

​ 数据构造方面，对于 B-tree 和 R-tree 索引的数据表，我们采用 PostgreSQL 自带的数据生成函数 generate_series 进行快速数据生成。以生成一百万条数据的数据表为例，我们使用的生成语句具体如下：

• B-tree 数据生成语句

create table btree1m(id integer, name text);
insert into btree1m(id, name)
select s.id, substring(md5(random()::varchar), 2, 8)
from generate_series (1, 1000000) as s(id)
order by random();

• R-tree 数据生成语句

create table rtree1m(id integer, p point);
insert into rtree1m(id, point)
select s.id, point(ceil(random()*10000), ceil(random()*10000))
from generate_series (1, 1000000) as s(id);

​ 对于 RD-tree，由于其数据类型（文档）要求比较特殊，仅使用 generate_series 无法满足要求，因此我们使用 python 中的 psycopg2库，先从含有 $1087$ 个单词的文档中随机抽取单词组成字符串，再插入数据表中，待数据插入完成后，统一使用 to_tsvector 语句生成词素，以完成数据构造，具体生成代码如下：

• RD-tree 数据生成语句

def generate_rdtree_data(filename):
    file = open(filename,"r",encoding="utf_8")
    raw_data = file.read()
    file.close()
    word_sets = raw_data.split(" ",1085)
    n = len(word_sets)


    conn = psycopg2.connect("dbname=gist_pj user=postgres password=123456")
    cur = conn.cursor()

    tables = ['rdtree1m','rdtree2m','rdtree5m','rdtree10m']
    data_nums = [1000000, 2000000, 5000000, 10000000]

    for i, table in enumerate(tables):
        print("Creating %s..."%(table))
        cur.execute('create table ' + table + '(id integer, words text);')
        conn.commit()
        print("%s created. Start inserting..."%(table))

        for j in range(data_nums[i]):
            word_num = random.randint(1, 20)
            words = []
            for k in range(word_num):
                idnum = random.randint(1, n - 1)
                words.append(word_sets[idnum])
            words = ' '.join(words)

            cur.execute('insert into ' + table + '(id, words) values(' + str(j) + ', \'' + words + '\');')
            conn.commit()
            if (j+1) %100000 == 0:
                print("Inserted %d words into %s"%(j+1,table))
        print("%s insert completed"%(table))

def to_tsvector():
    conn = psycopg2.connect("dbname=gist_pj user=postgres password=123456")
    cur = conn.cursor()

    tables = ['rdtree1m','rdtree2m','rdtree5m','rdtree10m']
    for table in tables:
        cur.execute('alter table ' + table + ' add words_tsv tsvector;')
        print("words_tsv added successful for %s"%(table))

        cur.execute('update ' + table + ' set words_tsv = to_tsvector(words);')
        print("words_tsv set successful for %s"%(table))
        conn.commit()

​ 最后生成的数据表样式如下（以1M数据表为例）：

• B-tree

• R-tree

• RD-tree

1.2 实验过程

​ 在 PostgreSQL 中自带原生的 B-tree索引和 R-tree 索引，但是没有原生的 RD-tree 索引（由Gist实现），因此本次性能分析实验我们使用 Gist 实现的 B-tree 索引和原生 B-tree索引、Gist 实现的 R-tree 索引和原生 R-tree索引以及 RD-tree 索引与无索引扫描进行性能比较。

​ 本次性能分析实验主要比较查询语句的性能，具体如下

• B-tree 会进行等值查询（=）、非等值查询（>, <）、查询后排序三项
• R-tree 进行范围查询（<@）以及KNN排序（$\leftrightarrow$）
• RD-tree 进行匹配查询（@@）

​ 每种查询语句会在每个数据表上分别执行多次，取平均值作为查询性能的表示以减小误差，同时可以观察查询次数对查询性能的影响。其中等值查询会分别进行 $100/1000/10000/100000$ 次，其余查询分别进行 $10/100/1000$ 次。每次查询时，查询条件均由 python 脚本随机生成。

2. B-tree 索引性能分析

2.1 等值查询

​ 我们分别使用 PostgreSQL 原生的 B-tree 索引（以下由B-tree代替）和由 Gist 实现的 B-tree 索引（以下由 Gist 代替）在四种规模（$1M/2M/5M/10M$）的数据表上分别进行了 $100/1000/10000/100000$ 次查询，以平均执行时间（ms）作为性能衡量标准，结果如下表所示：

	数据量（M=百万）	查询次数
		100	1000	10000	100000
B-tree	1M	0.03318	0.024798	0.018192	0.012111
	2M	0.05135	0.03864	0.021669	0.012036
	5M	0.06037	0.052307	0.031731	0.024
	10M	0.06896	0.057676	0.044845	0.034928
Gist	1M	0.07688	0.049448	0.028194	0.023334
	2M	0.09679	0.047306	0.038662	0.029991
	5M	0.10706	0.061588	0.060014	0.039931
	10M	0.14233	0.121944	0.071411	0.058829

​ 从上表可以看出，在不同查询次数下，B-tree 和 Gist 都存在一定的性能差距，这里我们以十万次查询的性能为例：

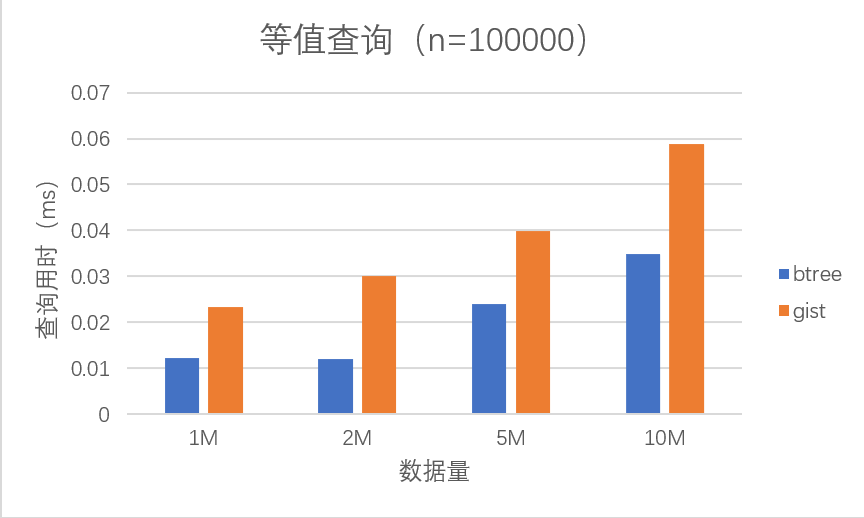
​ 可以看到：随着数据量逐渐增大，两种索引的查询时间都有所增加，但在四种数据集下，Gist 的查询时间都是 B-tree 的==两倍==左右。关于这一点其实在 PostgreSQL 的官方文档已有说明：使用 Gist 实现的 B-tree 性能并不会优于原生。在之后的非等值查询和排序实验中也能够发现，Gist 的性能相对 B-tree 有较明显的劣势。

​ 同时我们还注意到，随着查询次数的增加，两种索引的查询速度都有变快的趋势。以 B-tree 为例：

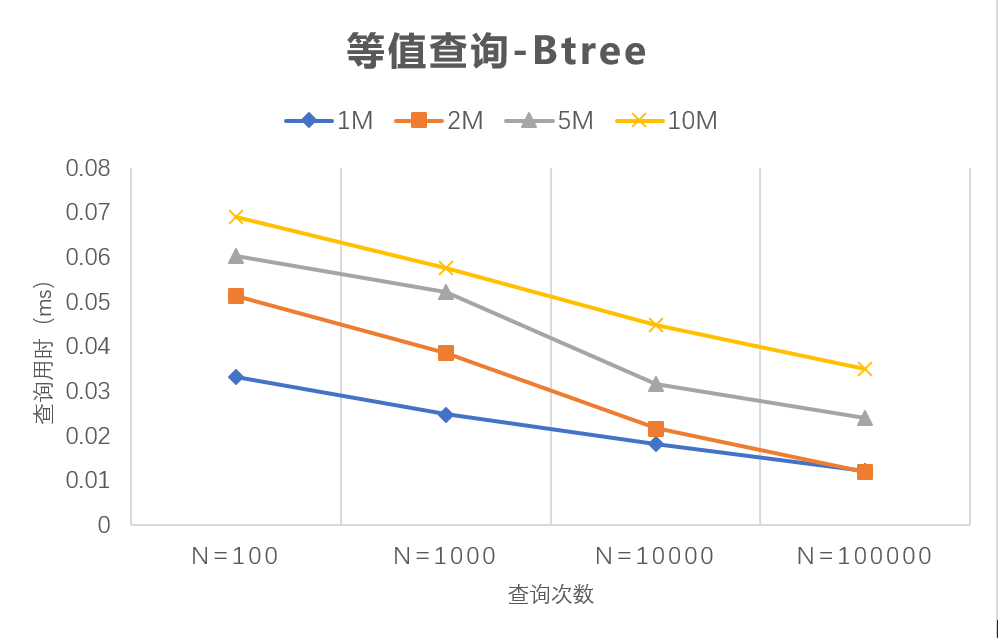
​ 可以看到，在四种数据集下，随着查询次数的增加，B-tree 索引的查询时间都有逐渐缩短的趋势。我们猜测这是因为 PostgreSQL 会将查询完成的数据项放入缓存中，若下次再次查询到此项可以加速访问。而随着查询次数增多，缓存的数据项也增多，查询命中率也增大，最终造成这种现象。

2.2 非等值查询

​ 我们使用 B-tree 和 Gist 在四张数据表上进行了非等值查询，由于相较于等值查询而言耗时更长，因此我们将查询次数下调至$10/100/1000$次。

​ 同时在非等值查询情境下，我们观察到即使已经建立了索引，数据库依然倾向于使用顺序扫描或位图扫描的情况时有发生，因此我们增加了无索引时的查询性能实验进行对比，结果如下表所示：

	数据量	查询次数
		10	100	1000
B-tree	1M	61.979	67.41578	63.08512
	2M	150.8887	116.6069	122.6648
	5M	276.8287	408.0294	409.7867
	10M	821.6075	853.392	807.5114
Gist	1M	107.5504	77.20416	79.64227
	2M	201.8327	174.0398	184.9779
	5M	596.5293	552.2071	537.8044
	10M	772.0948	923.3244	1046.903
无索引	1M	91.2538	109.5809	99.35411
	2M	216.5602	206.1646	172.2122
	5M	473.8722	447.3681	457.0516
	10M	1170.888	871.7418	843.4366

​ 通过上述数据我们可以观察到，在非等值查询条件下，B-tree 的性能依然是整体优于 Gist，但是差距不再像等值查询时相差两倍那么明显。同时值得注意的是，无索引时的查询性能不再像等值查询时那样远远慢于有索引查询了。我们以 $1000$ 次查询的性能数据为例：

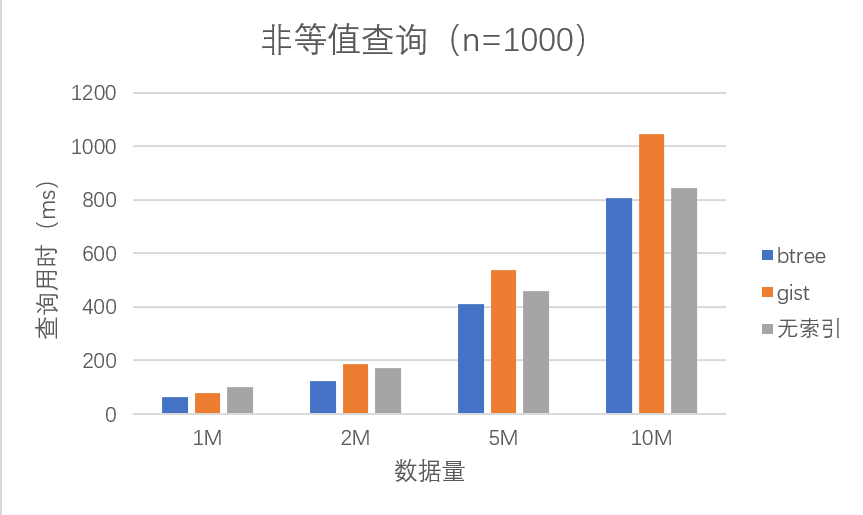
​ 从上表可以看出，B-tree 的查询性能依然整体优于无索引查询，但是差距并不明显；而 ==随着数据量的增大 Gist 的性能逐渐劣于无索引查询，并且差距越来越大==。我们认为这是由于非等值查询导致需要搜索的数据项增多，索引查询需要耗费更多时间在索引层，相比之下直接在数据层进行扫描可能会更快。可以预见，当数据量进一步提高时，B-tree 的性能也会逐渐劣于无索引扫描。

​ 我们还发现了另外一个不同于等值查询的现象：==在非等值查询中，随着查询次数的增加，查询性能可能不再像等值查询时那样获得提升，而是有所下降==，我们以 Gist 索引为例：

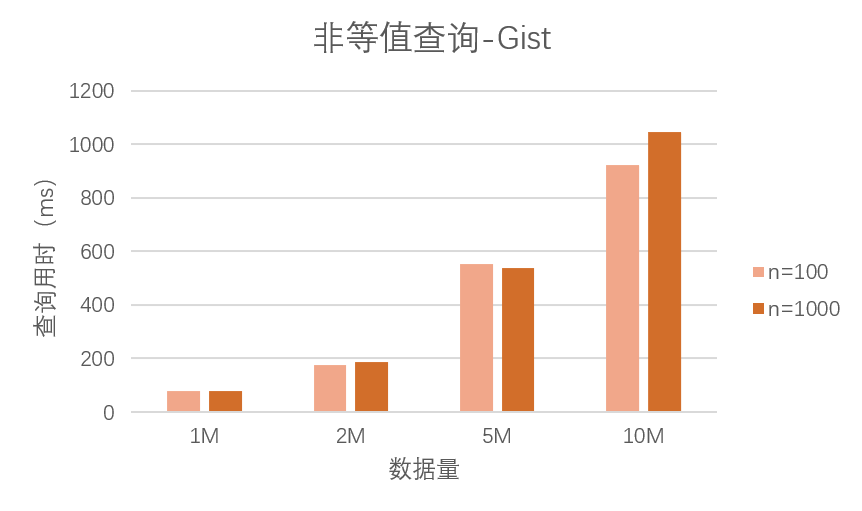
​ 当使用 Gist 索引时，查询 $1000$ 次的平均用时相比查询 $100$ 次而言反而有所升高，这在一千万规模的数据集上非常明显。我们认为这是因为非等值查询会占用更多的缓存空间，让数据库系统没法在缓存区保留已查询数据项，从而使查询性能不再提升，而是随着查询次数增多不断下降。

2.3 查询后排序

​ 我们使用 B-tree 和 Gist 在四张数据表上进行了增加排序的非等值查询，以下是实验结果：

	数据量	查询次数
		10	100	1000
B-tree	1M	177.2743	211.1747	196.704
	2M	482.5123	421.7937	400.1802
	5M	8856.351	7346.194	-
	10M	-	-	-
Gist	1M	456.3699	395.4264	358.9771
	2M	892.9861	746.8035	768.7536
	5M	10058.31	9237.658	-
	10M	-	-	-
无索引	1M	359.9617	369.8334	372.0706
	2M	730.1155	777.723	704.2577
	5M	1445.078	1919.576	2063.705
	10M	2851.832	3133.163	3026.798

注：由于查询用时过长，这里我们并未记录 $5$M-$1000$ 次查询结果以及 $10$M 数据量的查询结果

​ 显然，与不排序的非等值查询相比，增加排序的查询明显要耗费更多时间。出现这种情况，可能是因为在数据量过大的情况下，缓存已经不够用，需要更加频繁的 I/O 进行数据交换，从而严重影响了索引的性能。我们以 B-tree 为例：

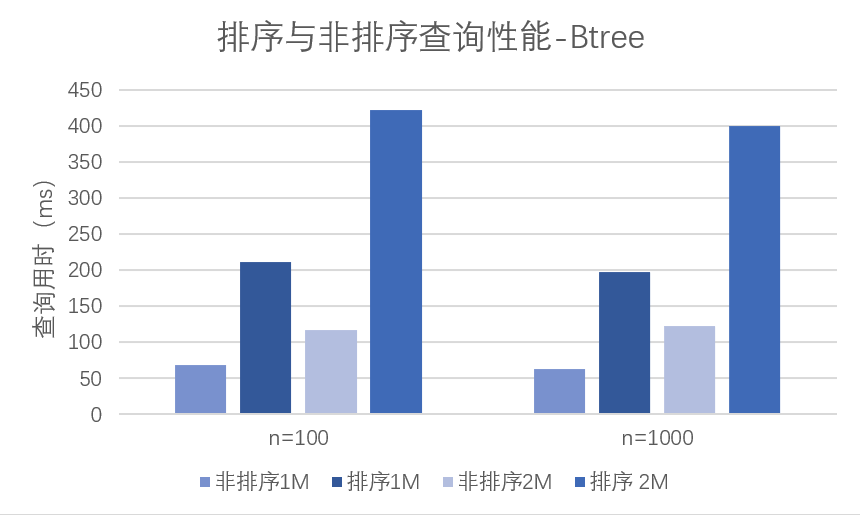
​ 带排序的非等值查询用时相比非排序增加了==三倍==左右，Gist 索引的情况也与之相似，除此以外，当数据量来到五百万以上时，索引查询用时陡升，以 Gist 为例：

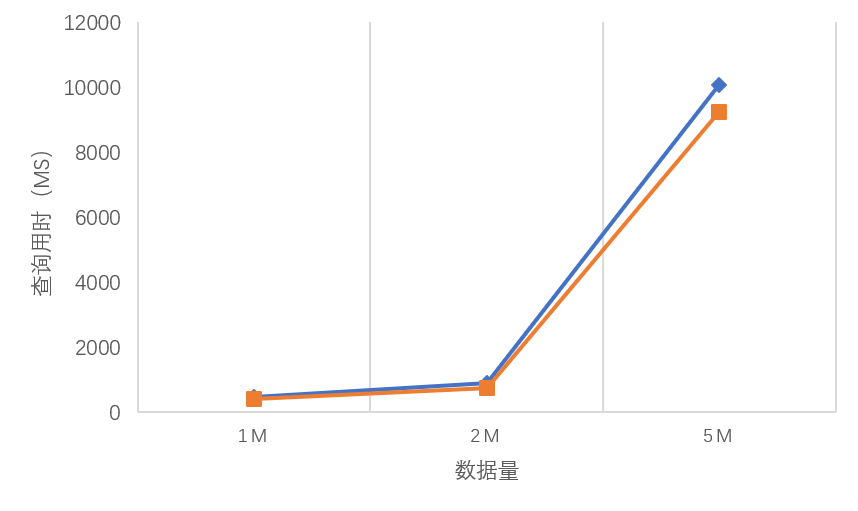
​ 下图给出了无索引情况下查询后排序时间与数据量间的关系，需要特别指出的是：**无索引查询排序的用时与数据量增加成正比，而且==并没有出现索引查询时性能急剧下降的情况==**。

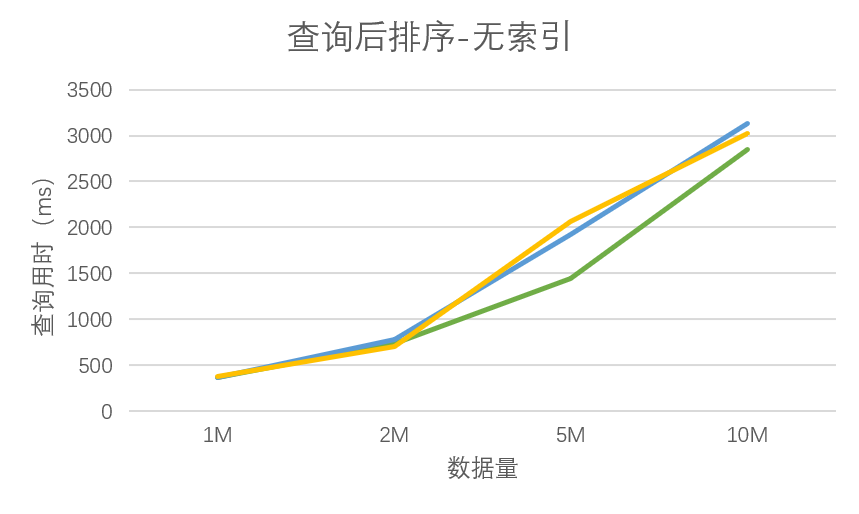
2.4 总结

​ 我们针对 B-tree 索引分别进行了等值查询、非等值查询和查询后排序，性能对比如下：

• Gist vs B-tree：实验结果显示 PostgreSQL 原生的 B-tree 在三种场景下性能均优于 Gist 实现的 B-tree

• Gist、B-tre vs 无索引：

  • 在等值查询中：两种索引的查询性能远远优于无索引查询
  • 在非等值查询中：随着数据量逐渐增大，索引查询的性能逐渐被无索引查询超越，尤其是在排序情景下，数据量足够大时，索引查询有可能会遭遇严重的性能瓶颈，导致性能断崖式下降，反而不使用索引的效果更好

3. R-tree 索引性能分析

3.1 范围查询

​ 我们分别使用 PostgreSQL 原生的 R-tree 索引（以下由 R-tree 代替）和由 Gist 实现的 R-tree 索引（以下由 Gist 代替）在四种规模（$1M/2M/5M/10M$）的数据表上分别进行了 $10/100/1000$ 次范围查询（<@ box），以平均执行时间（ms）作为性能衡量标准，结果如下表所示。需要说明的是，在使用 R-tree 索引的场景中，无索引扫描的性能要远远落后于索引扫描，因此在 R-tree 查询性能分析中我们不再对比无索引扫描性能。

	数据量	查询次数
		10	100	1000
R-tree	1M	49.6526	52.8736	47.26513
	2M	117.0581	120.0193	106.7405
	5M	1138.945	2136.78	2231.591
	10M	3743.78	6100.476	9216.125
Gist	1M	131.6751	97.39799	79.05427
	2M	139.4353	109.159	135.2277
	5M	1144.158	3627.209	2551.51
	10M	3458.488	6852.235	9485.287

​ 由上表可以看出，整体而言 R-tree 索引的范围查询性能要优于 Gist 索引。我们以 $1000$ 次查询次数的结果为例进行分析：

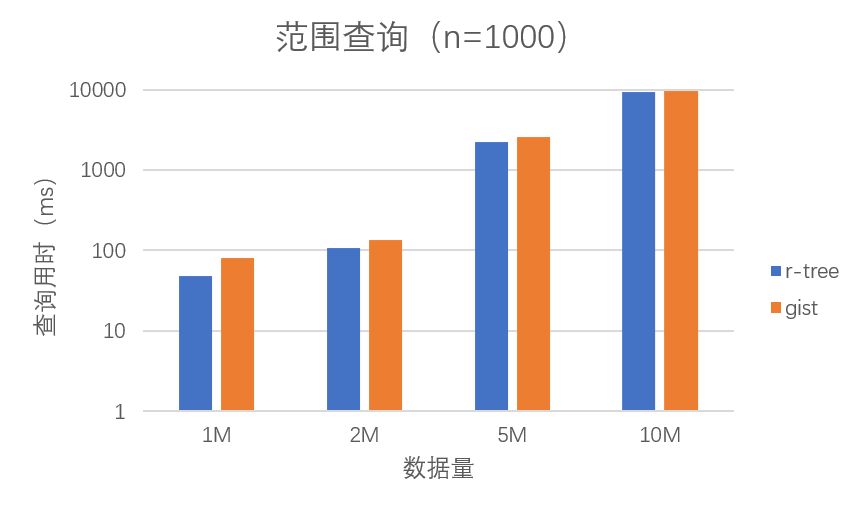
​ 可以看到，在四种规模的数据集中，R-tree 索引的性能都要略优于 Gist，但是差异并不十分明显，并且随着数据规模的增大，两者的性能逐渐接近。

​ 我们还发现，对于两种索引而言，在相同的数据集但不同查询次数下查询性能会出现较大波动，并且在数据集规模越大时这一现象越明显，同时使用 Gist 索引时这一现象也更明显。

​ 我们先分析 R-tree 索引。我们认为查询 $10$ 次的结果误差仍然比较大，因此更多考虑查询 $100$ 和 $1000$ 次的结果，比较分析如下：

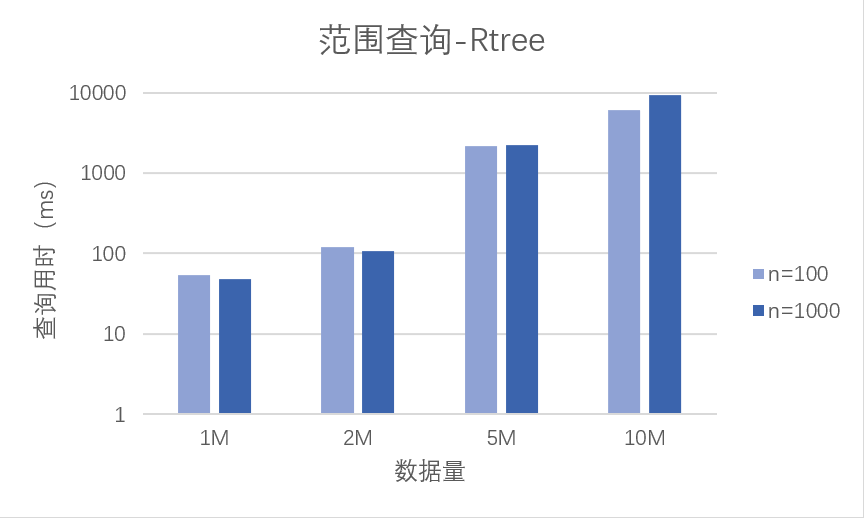
​ 由图表可知，当数据规模为一百万、两百万、五百万条时，不同查询次数下 R-tree 索引查询性能变化并不大，当数据规模来到一千万时，查询 $1000$ 次时的查询性能要明显劣于查询 $100$ 次时。造成这种现象的原因，我们认为和 B-tree 索引是类似的：当查询次数增多后，缓存空间被大量占用导致查询性能出现了瓶颈。

​ 我们再来看 Gist 索引的情况。和 R-tree 相比，Gist 索引的查询性能变化要更明显，如下图所示：

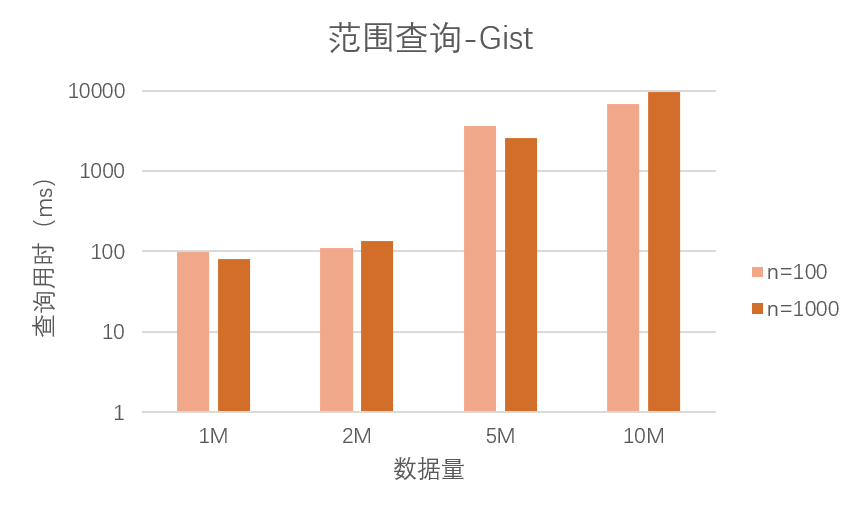
​ 可以看到，相比 R-tree 索引，Gist 索引在四种规模数据集中，不同查询次数下查询性能波动比较大。我们认为这可能是因为两种索引底层的缓存利用机制有所区别，而 R-tree 索引针对范围查询这一特定的应用场景进行了一定的优化，所以表现得更加稳定。

3.2 KNN排序

​ 我们使用 R-tree 和 Gist 在四张数据表上进行了 KNN 排序，其中每张表返回的 point 数量与该表的规模正成比（数据量/$100$），以更好地体现不同规模数据集下两种索引性能表现的差异，结果如下表所示：

	数据量	查询次数
		10	100	1000
R-tree	1M	30.0405	13.84511	11.68973
	2M	43.0087	24.04613	23.02512
	5M	265.9871	243.214	261.8839
	10M	736.0935	696.9722	662.0441
Gist	1M	17.9497	11.12343	10.8992
	2M	39.178	22.71717	22.4646
	5M	240.5831	239.0794	239.3458
	10M	671.5387	650.6201	658.2245

​ 整体上看，两种索引在 KNN 排序场景下的性能差距并不大，Gist 的性能要略优于 R-tree。我们以 $1000$ 次查询结果为例：

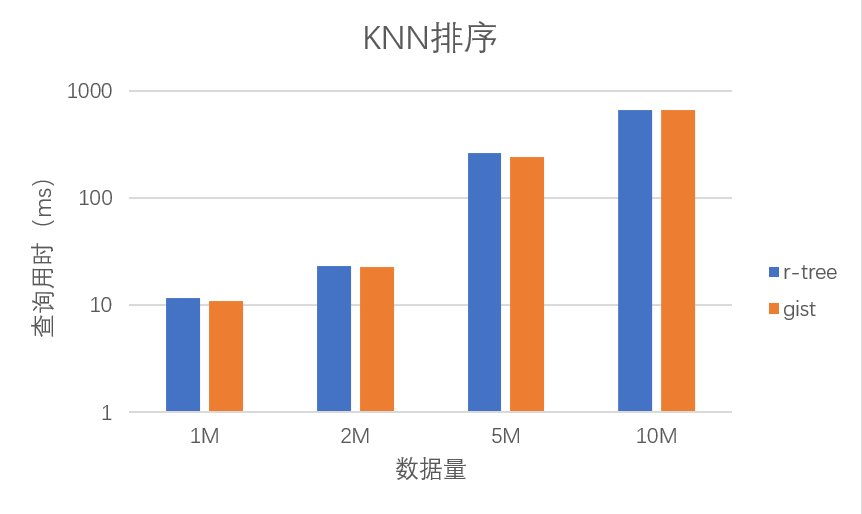
​ 可以看到两种索引的查询用时在四个规模的数据集下都比较接近，Gist 相较而言要略快一些。并且不同查询次数对两种索引的性能影响也微乎其微。

3.3 总结

​ 我们针对 R-tree 索引进行了范围查询和 KNN 排序两种场景下的性能实验，结果显示 PostgreSQL 原生的 R-tree 与 Gist 实现的 R-tree 性能差异并不如 B-tree 那么明显

• 在 KNN 排序场景下，两者的查询性能几乎相同
• 在范围查询中，Gist 在不同查询次数下性能波动比较大，而 R-tree 更加稳定，我们认为 R-tree 针对特定应用场景对缓存利用进行了一些优化以获得更稳定的性能

4. RD-tree 索引性能分析

4.1 全文检索

​ 由于 PostgreSQL 并没有原生的 RD-tree 索引，只有通过 Gist 实现的 RD-tree 索引，因此本节我们仅进行了 Gist 索引与无索引查询的性能对比实验。

​ 我们通过 python 脚本，从含有 $1087$ 个单词的文本中以随机数量随机抽取单词并组合成句子，分别生成了含有一百万、两百万、五百万数据项的数据集，并在这些数据集上进行了全文检索（匹配查询），查询用时结果如下：

	数据量	查询次数
		10	100	1000
Gist	1M	402.1559	467.6958	505.8494
	2M	1323.648	1351.347	1399.162
	5M	2755.076	3912.203	3888.738
无索引	1M	941.5422	1024.426	1144.391
	2M	1749.347	2744.705	1780.661
	5M	3277.635	3398.889	4955.399

​ 由于查询 $10$ 次的结果误差依然比较大，因此我们更多考虑查询 $100/1000$次的结果进行性能分析：

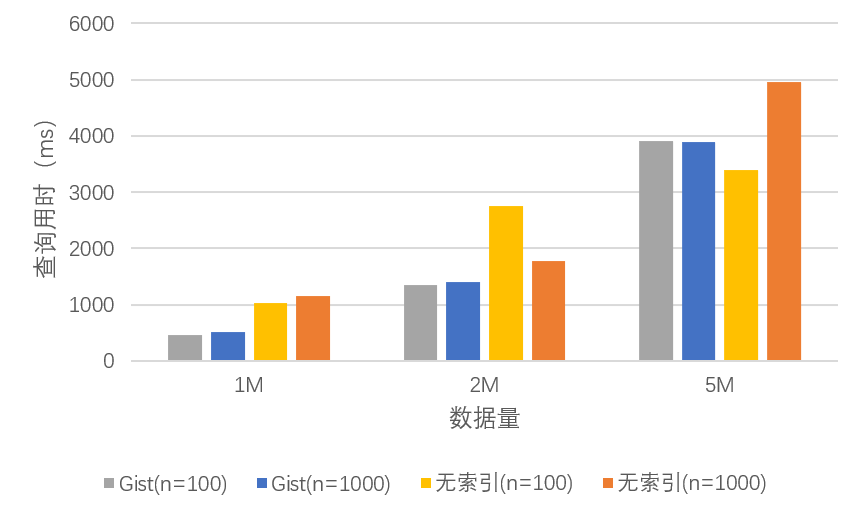
​ 从上图可以看出，当数据量不大时（一百万条），Gist 索引的查询性能要远快于无索引的查询性能，约为==两倍==左右。而随着数据量逐渐增大，两者的差距开始不断缩小。

​ 值得注意的是：在无索引查询的性能数据中，当查询次数为 100 次时，在两百万和五百万的数据集上出现==比较大的数据波动==，与查询次数为 1000 次的性能数据差异较大。

4.2 总结

​ 通过在三种不同规模的数据集上分别进行 Gist 索引和无索引的全文检索后，我们发现 Gist 索引的性能在小规模数据集上明显优于无索引查询，而当数据集不断增大时，两者的性能差距逐渐缩小，但是 Gist 索引依然优于无索引查询性能。

四、总结

• 准备工作
  • 性能指标：首先我们分析了一条 SQL 语句的处理过程，发现通过 EXPLAIN 命令可以查看规划器生成的查询计划，里面提供了大量统计信息，这里我们选用执行时间作为本次性能分析实验评判的主要标准，以访问内存/Cache的次数和索引使用情况作为辅助指标
  • 索引测试：然后我们按照官方文档，测试了 PostgreSQL 中的原生 B-tree 索引对性能的提升，以及 Gist 索引在三种应用场景下对性能的提升：几何类型检索（Gist 实现的 R-tree）、标量类型排序（Gist 实现的 B-tree）和全文检索（Gist 实现的 RD-tree）。其中我们发现由于系统内部自动优化，当数据量比较大时并没有使用索引扫描，实际使用的是位图扫描，因此需要额外进行设置来禁止位图扫描，索引测试为后续的性能分析实验排除了自动优化等可能带来的潜在干扰
• 主要工作：我们使用 Gist 实现的 B-tree、R-tree 和 RD-tree 对比了 PostgreSQL 中原生的索引以及无索引扫描在各种特定场景下的查询性能，包括 1) B-tree 的等值查询、非等值查询、排序；2) R-tree 的范围查询、KNN 排序；3) RD-tree 的全文检索
• 实验结论
  • Gist 实现的 B-tree 和 R-tree 索引在对应的场景下其查询性能相比原生索引并没有优势，尤其是 B-tree 索引，在三种场景下均全面落后于原生索引
  • 对于 Gist 实现的 RD-tree 索引，其查询性能在小规模数据集上明显优于无索引查询，而随着数据集规模的增大，两者的差距会不断缩小
  • 虽然 Gist 索引相比原生索引在性能上并无显著优势，但得益于 Gist 结构的泛用性和可扩展性，使得 Gist 能够执行更加复杂的任务，这是 B-tree、R-tree 等原生索引无法企及的优势
  • 另外，本次实验中我们还发现，不论是 Gist 索引，还是其它原生索引在面对较大规模的数据集时，都存在性能大幅下降的情况，我们认为这可能是因为索引扫描本身就需要占用更多的缓存空间，当数据规模过大时造成了缓存空间不够的情况，需要系统做更频繁的数据交换，使得性能遇到瓶颈。所以我们在对数据表建立索引时，应当时刻关注系统资源利用情况，以免遭遇类似性能问题