CoderZQYのBlog

个人不定期更新的学习周报

0%

finite_automaton

发表于 分类于

编译原理实验2——正则表达式->NFA->DFA->MFA

1、词法分析理论基础：有穷自动机（FA）

1.1 起源与定义

  • 有穷自动机(Finite Automata，FA)由两位神经物理学家MeCuloch和Pitts于1948年首先提出，是对一类处理系统建立的数学模型；
  • 这类系统具有一系列离散的输入输出信息和有穷数目的内部状态（状态：概括了对过去输入信息处理的状况）；
  • 系统只需要根据当前所处的状态和当前面临的输入信息就可以决定系统的后继行为。每当系统处理了当前的输入后，系统的内部状态也将发生改变。

1.2 FA分类

  • 确定的FA（Deterministic finite automata, DFA）
  • 非确定的FA（Nondeterministic finit automata, NFA）

1.3 确定的有穷自动机（DFA）

DFA被定义为一个五元组：M = ( S , Σ , δ , S0 , F )

  • S：有穷状态集；
  • Σ：输入字母表，即输入符号集合。假设ε不是Σ中的元素；
  • δ：将S×Σ映射到S的转换函数。∀ s ∈ S , a ∈ Σ , δ ( s , a ) 表示从状态s出发，沿着标记为a的边所能到达的状态（即状态S对应于输入符号的后继状态）；
  • S0：开始状态（或初始状态），S0∈S；
  • F：接收状态（或终止状态）集合，F⊆S。

1.4 非确定的有穷自动机（NFA）

NFA被定义为一个五元组：M = ( S , Σ , δ , S0 , F )

  • S：有穷状态集；
  • Σ：输入字母表，即输入符号集合。假设ε不是Σ中的元素；
  • δ：将S×Σ映射到S的转换函数。∀ s ∈ S , a ∈ Σ , δ ( s , a ) 表示从状态s出发，沿着标记为a的边所能到达的状态（即状态S对应于输入符号的后继状态）；
  • S0：开始状态（或初始状态）集合，S0⊆S；
  • F：接收状态（或终止状态）集合，F⊆S。

1.5 DFA和NFA的等价性

  • 对任何非确定的有穷自动机N ，存在定义同一语言的确定的有穷自动机D；
  • 对任何确定的有穷自动机D ，存在定义同一语言的非确定的有穷自动机N；

2、算法1：NFA确定化为DFA

DFA确定化的核心算法： 子集法

通俗的说：首先明确，

  1. NFA中的多个状态，共同组成了DFA中的多个状态。
  2. 我们先将NFA的初态集的闭包入队，然后BFS
  3. 每次从queue中取出一个状态集，用字母表的每个字母对其进行一次转换后取闭包（ε-closure(move(State))），如果产生新状态则入队，继续BFS。

其中，较为关键是基于一次转化函数的move、以及ε-closure闭包函数。代码中专门有注释说明。

2.1 首先定义NFA和DFA的JavaBean类

1
2
3
4
5
6
7
8
9
10
import java.util.List;

public class NFA {
    private List<Integer> S;    	// 状态集
    private char[] cigama;     		// 字母表
    private String[][] convert; 	// 转换函数
    private List<Integer> S0;   	// 初态集
    private List<Integer> F;    	// 终态集
    // setter和getter这里省略...
}
1
2
3
4
5
6
7
8
9
10
import java.util.List;

public class DFA {
    private List<Integer> S;     	// 状态集
    private char[] cigama;     	 	// 字母表
    private String[][] convert;  	// 转换函数
    private int S0;              	// 唯一初态
    private List<Integer> F;     	// 终态集
	// setter和getter这里省略...
}

2.2 子集法核心逻辑实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
import java.util.*;

public class NTD {
    /**
 	 * definite:【子集法】将NFA确定化为DFA
     * @param nfa 输入nfa
     * @return    返回dfa
     *
     * 伪代码逻辑：
     *  DFA状态集合S(注：S的每个成员又都是NFA的状态state的集合)
     *  Queue 临时队列queue;
     *  NFA的初态集S(S0)的闭包入队;
     *  while(队不空):
     *      取出当前状态集currStates;
     *      for 每个输入字母 in cigama:
     *             nextStates = ε-closure(move(currStates, letter));
     *             if(S 不包含 nextStates) :
     *                  则nextStates入队
     *
     *  最终的S即为确定化生成的DFA的状态集
     */
    public DFA definite(NFA nfa){
        List<Integer> States = nfa.getS0();
        char[] cigama = nfa.getCigama();
        String[][] convert = nfa.getConvert();
        List<Integer> F = nfa.getF();

        DFA dfa = new DFA();
        List<Integer> S = new ArrayList<>();             // DFA状态集合(已重命名)
        int s = 0;                                       // 用于DFA状态集的重命名
        List<String[]> listConvert = new ArrayList<>();        // 用于暂存转换函数
        List<Integer> listF = new ArrayList<>();         // 用于暂存终态集

        Set<List<Integer>> set = new HashSet<>();               // 状态集临时集合
        Queue<List<Integer>> queue = new LinkedList<>();        // 状态集临时队列
        Map<List<Integer>, Integer> map = new HashMap<>();      //「状态集」向「命名」的映射

        List<Integer> closure_S = closure(States, convert);     //闭包运算，获取当前真正状态集
        S.add(s);
        map.put(closure_S, s++);
        queue.add(closure_S);
        System.out.println("====================process====================");
        while(!queue.isEmpty()){                  // BFS
            List<Integer> currStates = queue.poll();
            //打印状态生成过程
            System.out.print("原状态：" + currStates);
            System.out.print("\t新状态：");
            for(char letter : cigama){
                List<Integer> nextStates = closure(move(currStates, letter, convert), convert);
                if(nextStates.isEmpty()){
                    //System.out.println("Ø");
                    continue;
                }
                if(!containsS(set, nextStates)){
                    // 如果产生了一个新状态，就进行接下来的诸多操作
                    // 给它一个新名字并维护s、确定它是不是终态(包含NFA的终态)、入集合、入队
                    nextStates.sort(Comparator.comparing(Integer::intValue));
                    map.put(nextStates, s);
                    S.add(s);
                    if(!Collections.disjoint(nextStates, F)){
                        listF.add(s);
                    }
                    set.add(nextStates);
                    queue.add(nextStates);
                    s++;
                }
                System.out.print(nextStates+"\t");
                listConvert.add(new String[]{String.valueOf(map.get(currStates)), String.valueOf(letter), String.valueOf(map.get(nextStates))});
                System.out.print("转换函数："+map.get(currStates)+letter+map.get(nextStates)+";\t");
            }
            System.out.println();
        }
        // 下面是构造出DFA对象，作为返回值
        int len = S.size();
        String[][] newConvert = new String[len][len];
        for(String[] tmp : newConvert){
            Arrays.fill(tmp, "");
        }
        for(String[] arr : listConvert){
            newConvert[Integer.parseInt(arr[0])][Integer.parseInt(arr[2])] += arr[1];
        }
        dfa.setS(S);
        dfa.setCigama(cigama);
        dfa.setConvert(newConvert);
        dfa.setS0(0);
        dfa.setF(listF);
        return dfa;
    }

    /**
     * ε-closure闭包运算：某个状态集经过任意多个ε，得到当前的真正状态集
     * @param State 当前状态集
     * @return 当前真正的状态集(closureS)
     */
    private List<Integer> closure(List<Integer> State, String[][] convert){
        // 经过任意多个ε，因此BFS ！ ！ ！
        List<Integer> closureS  = new ArrayList<>();
        Queue<Integer> queue = new LinkedList<>();
        for(int i : State){
            queue.add(i);
            while (!queue.isEmpty()){
                int currState = queue.poll();
                for(int iNext = 0; iNext < convert.length; iNext++){
                    for(char c : convert[currState][iNext].toCharArray()){
                        if(c == 'ε' && !closureS.contains(iNext)){
                            closureS.add(iNext);
                            if(currState != iNext){
                                queue.add(iNext);
                            }
                        }
                    }
                }
            }
        }
        return closureS;
    }

    /**
     * move方法：当前状态集通过某个字母可以转化到的下一状态集（一步转换，没有进行ε-闭包运算）
     * @param State 当前的状态集
     * @return nextStates 返回下一状态集
     */
    private List<Integer> move(List<Integer> State, char letter, String[][] convert){
        List<Integer> nextStates = new ArrayList<>();
        for(int i : State){
            for(int iNext = 0; iNext < convert.length; iNext++){
                for(char c : convert[i][iNext].toCharArray()){
                    if(c == letter && !nextStates.contains(iNext)) {
                        nextStates.add(iNext);
                    }
                }
            }
        }
        return nextStates;
    }



    /**
     * 判断一个Set<List>是否包含某个List
     * @param set
     * @param list
     */
    private boolean containsS(Set<List<Integer>> set, List<Integer> list){
        for(List<Integer> l : set){
            if(listEquals(l, list)){
                return true;
            }
        }
        return false;
    }

    /**
     * 判断两个List集合是否相等（不考虑顺序）
     * @param list1
     * @param list2
     */
    private boolean listEquals(List<Integer> list1, List<Integer> list2){
        list1.sort(Comparator.comparing(Integer::intValue));
        list2.sort(Comparator.comparing(Integer::intValue));
        return list1.toString().equals(list2.toString());
    }

}

2.3 定义ReadNFAUtil工具类获取NFA五元组的信息

1. 准备一个NFA作为测试案例

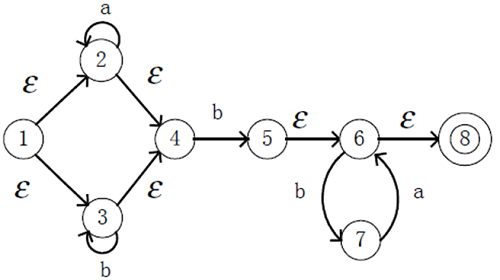
image-20210330155914801

2. 将对应的五元组写入txt文件

注意：状态从0开始定义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
S=01234567
cigama=ab
convert=0ε1
convert=0ε2
convert=1a1
convert=1ε3
convert=2b2
convert=2ε3
convert=3b4
convert=4ε5
convert=5ε7
convert=5b6
convert=6a5
S0=0
F=7

这里将其命名为NTD.txt

3. 定义ReadNFAUtil工具类，读入五元组信息

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
public class ReadNFAUtil {
    private static String[][] convert;
    public static NFA readFile(String filePath) {
        //以字符方式读取文本文件
        FileReader fis = null;
        BufferedReader br = null;
        NFA nfa = new NFA();
        try {
            fis = new FileReader(filePath);
            br = new BufferedReader(fis);
            String line;
            while ((line = br.readLine()) != null){
                String declare = line.split("=")[0];
                String value = line.split("=")[1];
                switch (declare){
                    case "S":readS(nfa,value);break;
                    case "cigama":readCigama(nfa,value);break;
                    case "convert":readConvert(nfa,value);break;
                    case "S0":readS0(nfa,value);break;
                    case "F":readF(nfa,value);break;
                }
            }
        } catch (Exception e) {
            e.printStackTrace();
        }finally {
            if(br != null){
                try {
                    br.close();
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
        }
        return nfa;
    }

    private static void readF(NFA nfa, String value) {
        List<Integer> list = new ArrayList<>();
        String[] strings = value.split("");
        for (String s : strings){
            list.add(Integer.parseInt(s));
        }
        nfa.setF(list);
    }

    private static void readS0(NFA nfa, String value) {
        String[] arr = value.split("");
        List<Integer> list = new ArrayList<>();
        for(String s : arr){
            list.add(Integer.parseInt(s));
        }
        nfa.setS0(list);
    }

    private static void readConvert(NFA nfa, String value) {
        String[] arr = value.split("");
        convert[Integer.parseInt(arr[0])][Integer.parseInt(arr[2])] += arr[1];
        nfa.setConvert(convert);
    }

    private static void readCigama(NFA nfa, String value) {
        char[] cigama = value.toCharArray();
        nfa.setCigama(cigama);
    }

    private static void readS(NFA nfa, String value) {
        List<Integer> list = new ArrayList<>();
        for(char ch : value.toCharArray()){
            list.add(Integer.parseInt(String.valueOf(ch)));
        }
        int n = list.size();
        nfa.setS(list);

        //init convert[][]
        convert = new String[n][n];
        for(String[] arr : convert){
            Arrays.fill(arr, "");
        }
        for(int i = 0; i < n; i++){
            convert[i][i] = "ε";
        }
    }
}

4. 定义DisplayUtils工具类，用于打印nfa、dfa对象

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
public class DisplayUtils {

    public static void displayS(NFA nfa){
        System.out.println(nfa.getS());
    }

    public static void displayCigama(NFA nfa){
        System.out.println(Arrays.toString(nfa.getCigama()));
    }

    public static void displayConvert(NFA nfa){
        String[][] convert = nfa.getConvert();
        for(int i = 0; i < convert.length; i++){
            for(int j = 0; j < convert.length; j++){
                if(convert[i][j].equals(""))  continue;
                for(char c : convert[i][j].toCharArray()){
                    if(i == j && c == 'ε')  continue;
                    System.out.print(String.valueOf(i) + c + j + "  ");
                }
            }
        }
        System.out.println();
    }

    public static void displayS0(NFA nfa){
        System.out.println(nfa.getS0());
    }

    public static void displayF(NFA nfa){
        System.out.println(nfa.getF());
    }


    public static void displayS(DFA dfa){
        System.out.println(dfa.getS());
    }

    public static void displayCigama(DFA dfa){
        System.out.println(Arrays.toString(dfa.getCigama()));
    }

    public static void displayConvert(DFA dfa){
        String[][] convert = dfa.getConvert();
        for(int i = 0; i < convert.length; i++){
            for(int j = 0; j < convert.length; j++){
                if(convert[i][j].equals("")) continue;
                for(char c : convert[i][j].toCharArray()){
                    if(c != 'ε'){
                        System.out.print(String.valueOf(i) + c + j + "\t");
                    }
                }
            }
        }
        System.out.println();
    }

    public static void displayS0(DFA dfa){
        System.out.println(dfa.getS0());
    }

    public static void displayF(DFA dfa){
        System.out.println(dfa.getF());
    }

}

2.4 定义测试类NTDTest

  1. 定义一个NTDTest类进行测试
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public class NTDTest {
    public static void main(String[] args) {
        //读入测试文件
        NFA nfa = ReadNFAUtil.readFile("src/编译原理/作业2/test/testFile/NTD.txt");
        DFA dfa = new NTD().definite(nfa);
        System.out.println("====================dfa====================");
        System.out.print("DFA状态集：");            DisplayUtils.displayS(dfa);
        System.out.print("DFA字母表：");            DisplayUtils.displayCigama(dfa);
        System.out.print("DFA状态转换函数：");       DisplayUtils.displayConvert(dfa);
        System.out.print("DFA唯一初态：");          DisplayUtils.displayS0(dfa);
        System.out.print("DFA终态集：");            DisplayUtils.displayF(dfa);
        System.out.println("====================end====================");
    }
}
  1. 测试结果如下：

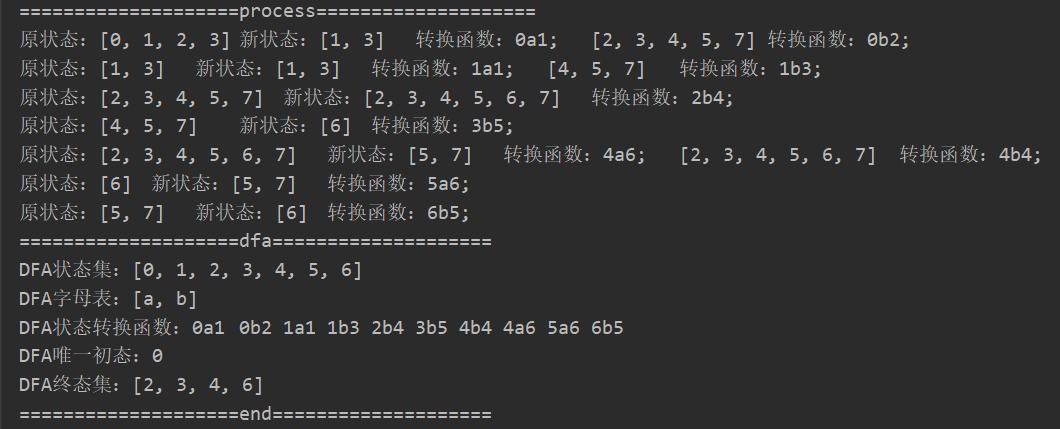
image-20210330161020361

  1. process过程对照结果

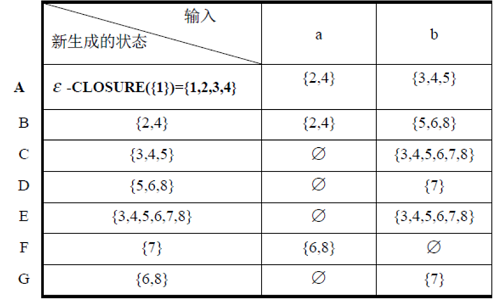
image-20210330161058735

注：这里的分组重新标号为0123...，对应图中的ABCD..

  1. 生成的dfa对照结果

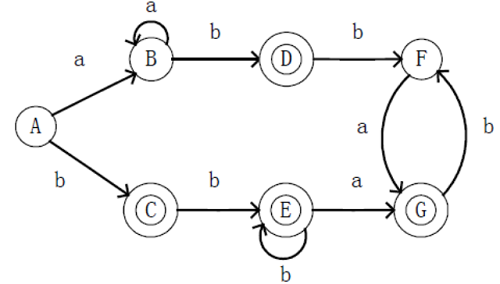
image-20210330161213124

  1. 结果正确，可测试多组案例，确认无误再往下进行

3、算法2：DFA最小化为MFA

注：DFA的最小化也称为：确定的有穷状态机的化简。

3.1 算法说明

DFA的最小化 = 消除无用状态 + 合并等价状态

  1. 消除无用状态这里是指删掉那些达到不了的状态。这不是我们的重点，DFS+HashSet不难实现。
  2. 其实关键在于合并等价状态。那么，怎样的两个状态是等价的呢？

状态的等价需要满足两个条件：

  1. 一致性条件：它们都是可接受状态或不可接受状态（即都是终态或非终态）
  2. 蔓延性条件：我们用所有的输入符号进行转化，它们都可以转化到等价的状态里

DFA最小化核心算法：分割法

算法步骤如下：：

  1. 先根据终态/非终态分为两组
  2. 然后对同一组中的状态，用所有输入符号去试着转化，如果转化不到一组，则再分
  3. 不断进行上述操作，直到每一组各自的状态集通过任何一个字母都不会转移到其他组

3.2 定义Group的JavaBeen类，用于分组

1
2
3
4
5
6
7
8
9
public class Group {
    public int groupID;
    public Set<Integer> stateSet;

    public Group(int groupID, Set<Integer> stateSet) {
        this.groupID = groupID;
        this.stateSet = stateSet;
    }
}

3.3 分割法核心逻辑实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
/**
 *【DFA的最小化】
 * 核心思路：
 *  1. 定义一个Group类，作为「分组」。
 *     Group有两个属性：groupID作为唯一标识；StateSet为该分组包含的状态集
 *  2. separate()方法的作用是，根据某个字母(letter)对分组集合(groupSet)进行彻底分裂
 *  3. 对于字母表中的每个字母，进行separate分裂
 *
 * 下面的论述有利于理解这个算法：
 *  1. HashMap做映射，是该算法的一个关键点。
 *     对于某个字母，一个分组(group)的所有状态(state)根据这个字母，用HashMap记录它们分别会被映射到哪个分组里，据此分裂。
 *     举个例子：{group1,[0, 1]}, {group2,[2, 3]}    (key是组，value是转化后指向该组的所有状态)
 *     0,1状态会转化到1组，2,3状态会转化到2组，据此，旧组分裂为了两个新组，然后删掉旧组，新组入队BFS
 *     如果这个哈希表的size==1，说明所有状态只能转化到一个组中，那么它们是等价的，不用删掉旧组，该组直接进入finalGroupSet最终分组
 *   2. groupID的作用是什么？为什么还要专门维护它？
 *      唯一标识。从1中看出，过程中不断进行着"删掉旧组，生成新组"的行为。维护这个ID主要是为了HashMap做映射
 *
 */
public class MinDFA {
    private int cnt = 0;

    public DFA minDFA(DFA dfa){
        List<Integer> S = dfa.getS();
        List<Integer> F = dfa.getF();
        String[][] convert = dfa.getConvert();
        char[] cigama = dfa.getCigama();

        S.removeAll(F);         // 全部状态集K - 终态集Z = 非终态集
        Group groupx = new Group(cnt++, new HashSet<>(S));
        Group groupy = new Group(cnt++, new HashSet<>(F));
        Set<Group> finalGroupSet = new HashSet<>();             // 最终分组
        Set<Group> curGroupSet;               // 此时的分组
        finalGroupSet.add(groupx);
        finalGroupSet.add(groupy);

        for(char letter : cigama){                                 // 对于每个字母
            curGroupSet = finalGroupSet;                            // 【最终分组】不断沦为【此时分组】
            finalGroupSet = separate(curGroupSet, letter, convert);       // 【此时分组】又分裂成新的【最终分组】
        }                                                           // 所有字母都用了一次后，成为名副其实的【最终分组】

        // 打印最终分组(一组中的状态等价)
        System.out.println("====================final groups====================");
        //重新编号
        renumber(finalGroupSet);
        //创建mfa，调用set赋值
        DFA mfa = new DFA();
        mfa.setS(getS(finalGroupSet.size()));
        mfa.setCigama(dfa.getCigama());
        mfa.setConvert(getConvert(finalGroupSet,dfa.getConvert()));
        mfa.setS0(findGroupID(dfa.getS0(),finalGroupSet));
        mfa.setF(findGroupIDs(dfa.getF(),finalGroupSet));
        return mfa;
    }

    private void renumber(Set<Group> finalGroupSet) {
        int n = finalGroupSet.size();
        //按照 0 ~ n-1 编号
        int number = 0;
        for(Group group : finalGroupSet){
            group.groupID = number++;
            System.out.println(group.groupID+":"+group.stateSet);
        }
    }

    private List<Integer> findGroupIDs(List<Integer> F, Set<Group> finalGroupSet) {
        List<Integer> list = new ArrayList<>();
        for(Group group : finalGroupSet){
            for (Integer f : F) {
                if(group.stateSet.contains(f) && !list.contains(group.groupID)){
                    list.add(group.groupID);
                }
            }
        }
        return list;
    }

    private String[][] getConvert(Set<Group> finalGroupSet, String[][] convert) {
        int n = finalGroupSet.size();
        String[][] newConvert = new String[n][n];
        for(String[] tmp : newConvert){
            Arrays.fill(tmp, "");
        }
        for (int i = 0; i < convert.length; i++) {
            for (int j = 0; j < convert.length; j++) {
                if(!convert[i][j].equals("")){
                    String[] strs = convert[i][j].split("");
                    int ii = findGroupID(i,finalGroupSet);
                    int jj = findGroupID(j,finalGroupSet);
                    for (int k = 0; k < strs.length; k++) {
                        if(!newConvert[ii][jj].contains(strs[k])){
                            newConvert[ii][jj] += strs[k];
                        }
                    }
                }
            }
        }
        return newConvert;
    }

    private int findGroupID(int i, Set<Group> finalGroupSet) {
       for(Group group : finalGroupSet){
           if(group.stateSet.contains(i)){
               return group.groupID;
           }
       }
       System.out.println("Search ERROR!");
       return -1;
    }

    private List<Integer> getS(int cnt) {
       List<Integer> list = new ArrayList<>();
       for (int i = 0; i < cnt; i++) {
           list.add(i);
       }
       return list;
    }

    private Set<Group> separate(Set<Group> groupSet, char letter, String[][] convert){
       Set<Group> finalGroupSet = new HashSet<>();
       Queue<Group> queue = new LinkedList<>(groupSet);

       while (!queue.isEmpty()){
           Group oldGroup = queue.poll();
           Map<Group, List<Integer>> map = new HashMap<>();  //根据指向的组，对状态Integer进行分类
           for(Integer state : oldGroup.stateSet){
               Group stateNextBelong = belong(state, letter, convert, groupSet);
               if(!map.containsKey(stateNextBelong)){
                   map.put(stateNextBelong, new ArrayList<>());
               }
               map.get(stateNextBelong).add(state);
           }
           if (map.size() == 1){   // 如果这些状态映射到了一个状态集(Group)中，则为最终分组
               finalGroupSet.add(oldGroup);
           }else{                  // 如果这些状态映射到了多个状态集(Group)中，则删除原先分组，创建多个新分组，并将新分组入队
               groupSet.remove(oldGroup);
               for(List<Integer> list : map.values()){
                   Group newGroup = new Group(cnt++, new HashSet<>(list));
                   groupSet.add(newGroup);
                   queue.add(newGroup);
               }
           }
       }
       return finalGroupSet;
    }

    /**
     * move方法: 返回唯一后继状态（-1表示没有后继状态）
     */
    private int move(int state, char letter, String[][] f){
        for(int nextState = 0; nextState < f.length; nextState++){
            for(char c : f[state][nextState].toCharArray()){
                if(c == letter){
                    return nextState;
                }
            }
        }
        return -1;
    }

    /**
     * beLong方法: 某状态(state)经过字母(letter)一次转化(move)后，所属于的当前分组(group)
     */
    private Group belong(int state, char letter, String[][] f, Set<Group> groupSet){
        int newState = move(state, letter, f);
        for(Group group : groupSet){
            if(group.stateSet.contains(newState)){
                return group;
            }
        }
        return null;
    }

}

3.4 定义ReadDFAUtil工具类获取DFA五元组的信息

1. 准备一个DFA作为测试案例

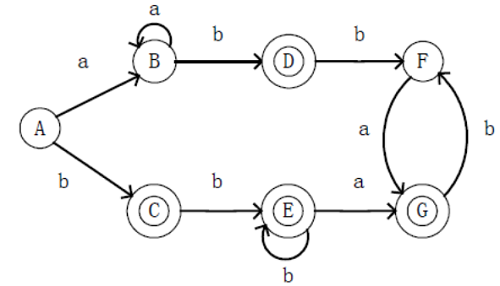
image-20210330204513283

2. 将对应的五元组写入txt文件

注意：状态从0开始定义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
S=0123456
cigama=ab
convert=0a1
convert=1a1
convert=1b3
convert=3b5
convert=5a6
convert=6b5
convert=0b2
convert=2b4
convert=4b4
convert=4a6
S0=0
F=2346

这里将其命名为MinDFA.txt

3. 定义ReadDFAUtil工具类，读入五元组信息

注：和ReadNFAUtil基本相同，只有读入S0有区别，此处代码略

4. DisplayUtils工具类已在算法1中定义

3.5 定义测试类MinDFATest

  1. 定义一个NTDTest类进行测试
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class MinDFATest {
    public static void main(String[] args) {
        DFA dfa = ReadDFAUtil.readFile("src/编译原理/作业2/test/testFile/MinDFA.txt");
        print("dfa",dfa);
        DFA mfa = new MinDFA().minDFA(dfa);
        print("mfa",mfa);
    }
    static void print(String tagName, DFA dfa){
        System.out.println("===================="+tagName+"====================");
        System.out.print("DFA状态集：");            DisplayUtils.displayS(dfa);
        System.out.print("DFA字母表：");            DisplayUtils.displayCigama(dfa);
        System.out.print("DFA状态转换函数：");       DisplayUtils.displayConvert(dfa);
        System.out.print("DFA唯一初态：");          DisplayUtils.displayS0(dfa);
        System.out.print("DFA终态集：");            DisplayUtils.displayF(dfa);
    }
}
  1. 测试结果如下：

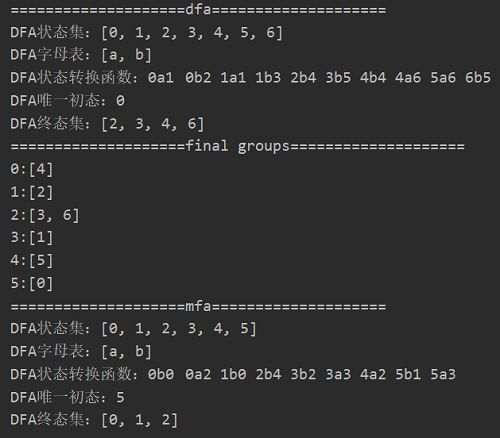
image-20210330205255128

注：这里的分组重新标号为0123...，而不是图中的ABCD..

  1. 生成的mfa对照结果

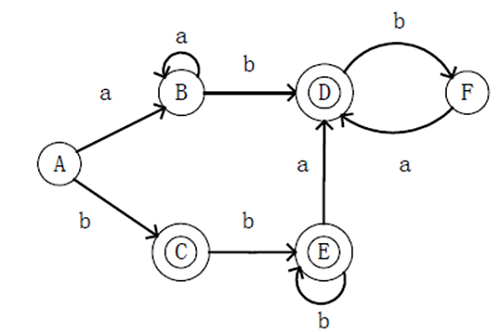
image-20210330205400590

  1. 结果正确，可测试多组案例，确认无误再往下进行

3、算法3：正则表达式转换为NFA

3.1 首先定义Node和Edge的JavaBeen类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Node {
    private int id;
    private static int ID = 0;

    public Node() {
        this.id = ID++;
    }

    public int getId() {
        return id;
    }

    public static void reset(){
        ID = 0;
    }

    @Override
    public String toString() {
        return id + "";
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class Edge {
    private Node begin;
    private Node end;
    private String label;
    private Edge edge;
    
    public Edge() {
        super();
    }
    public Edge(Node begin, Node end) {
        super();
        this.begin = begin;
        this.end = end;
    }
    public Edge(Node begin, Node end, String label) {
        super();
        this.begin = begin;
        this.end = end;
        this.label = label;
    }  
    // setter和getter这里省略... 
    @Override
    public String toString() {
        return "Edge [begin="+begin+", end="+end+", label="+label+"]";
    }
}

3.2 定义Graph类用于构造NFA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
public class Graph {
    private List<Edge> edges;
    private Node start;
    private Node end;

    public Graph() {
        edges = new ArrayList<>();
    }

    public List<Edge> getEdges() {
        return edges;
    }

    public Node getStart() {
        return start;
    }

    public void setStart(Node start) {
        this.start = start;
    }

    public Node getEnd() {
        return end;
    }

    public void setEnd(Node end) {
        this.end = end;
    }

    public void reset() {
        Node.reset();
    }

    /**
     * 根据操作符和操作对象来进行连接、联合、闭包处理
     * 由参数来判断调用构建NFA的函数
     * 处理a*时会调用处理单字符闭包的函数，对应的也有处理NFA闭包的函数
     */
    public void Star(Object obj) {
        if (obj.getClass().getName().equals(Graph.class.getName())) {
            addStar((Graph) obj);
            return;
        }
        if (obj.getClass().getName().equals(Character.class.getName())) {
            addStar((Character) obj);
            return;
        } else {
            throw new RuntimeException("You have an error in your Regex syntax");
        }
    }

    public void Union(Object obj1, Object obj2) {
        if (obj1.getClass().getName().equals(Character.class.getName())) {
            if (obj2.getClass().getName().equals(Graph.class.getName())) {
                addUnion((Character) obj1, (Graph) obj2);
                return;
            }
            if (obj2.getClass().getName().equals(Character.class.getName())) {
                addUnion((Character) obj1, (Character) obj2);
                return;
            }
        }
        if (obj1.getClass().getName().equals(Graph.class.getName())) {
            if (obj2.getClass().getName().equals(Graph.class.getName())) {
                addUnion((Graph) obj1, (Graph) obj2);
                return;
            }
            if (obj2.getClass().getName().equals(Character.class.getName())) {
                addUnion((Graph) obj1, (Character) obj2);
                return;
            }
        } else {
            throw new RuntimeException("You have an error in your Regex syntax");
        }
    }

    public void Concat(Object obj1, Object obj2) {
        if (obj1.getClass().getName().equals(Character.class.getName())) {
            if (obj2.getClass().getName().equals(Graph.class.getName())) {
                addConcat((Character) obj1, (Graph) obj2);
                return;
            }
            if (obj2.getClass().getName().equals(Character.class.getName())) {
                addConcat((Character) obj1, (Character) obj2);
                return;
            }
        }
        if (obj1.getClass().getName().equals(Graph.class.getName())) {
            if (obj2.getClass().getName().equals(Graph.class.getName())) {
                addConcat((Graph) obj1, (Graph) obj2);
                return;
            }
            if (obj2.getClass().getName().equals(Character.class.getName())) {
                addConcat((Graph) obj1, (Character) obj2);
                return;
            }
        } else {
            throw new RuntimeException("You have an error in your Regex syntax");
        }
    }

    /**
     * 处理NFA闭包
     */
    public void addStar(Graph graph) {
        Node begNode = new Node();
        Node endNode = new Node();
        Edge edge1 = new Edge(begNode, endNode, "ε");
        Edge edge2 = new Edge(begNode, graph.getStart(), "ε");
        Edge edge3 = new Edge(graph.getEnd(), endNode, "ε");
        /**
         * 改动的地方
         */
        Edge edge4 = new Edge(graph.getEnd(), graph.getStart(), "ε");
        this.edges.addAll(graph.getEdges());
        this.edges.add(edge1);
        this.edges.add(edge2);
        this.edges.add(edge3);
        /**
         * 改动的地方
         */
        this.edges.add(edge4);
        this.start = begNode;
        this.end = endNode;
    }

    /**
     * 处理单字符闭包
     */
    public void addStar(Character character) {
        Node nodeCenter = new Node();
        Node nodebeg = new Node();
        Node nodeend = new Node();
        Edge edgeLink = new Edge(nodeCenter, nodeCenter, character.toString());
        Edge edgeεBeg = new Edge(nodebeg, nodeCenter, "ε");
        Edge edgeεEnd = new Edge(nodeCenter, nodeend, "ε");
        this.edges.add(edgeLink);
        this.edges.add(edgeεBeg);
        this.edges.add(edgeεEnd);
        this.start = nodebeg;
        this.end = nodeend;
    }

    public void addUnion(Character character, Graph graph) {
        Node begNode = new Node();
        Node endNode = new Node();
        Edge edge1 = new Edge(begNode, graph.getStart(), "ε");
        Edge edge2 = new Edge(graph.getEnd(), endNode, "ε");
        Edge edge3 = new Edge(begNode, endNode, character.toString());
        this.edges.addAll(graph.getEdges());
        this.edges.add(edge1);
        this.edges.add(edge2);
        this.edges.add(edge3);
        this.start = begNode;
        this.end = endNode;
    }

    public void addUnion(Graph graph, Character character) {
        Node begNode = new Node();
        Node endNode = new Node();
        Edge edge1 = new Edge(begNode, graph.getStart(), "ε");
        Edge edge2 = new Edge(graph.getEnd(), endNode, "ε");
        Edge edge3 = new Edge(begNode, endNode, character.toString());
        this.edges.addAll(graph.getEdges());
        this.edges.add(edge1);
        this.edges.add(edge2);
        this.edges.add(edge3);
        this.start = begNode;
        this.end = endNode;
    }

    public void addUnion(Graph graph1, Graph graph2) {
        Node begNode = new Node();
        Node endNode = new Node();
        Edge edge1 = new Edge(begNode, graph1.getStart(), "ε");
        Edge edge2 = new Edge(begNode, graph2.getStart(), "ε");
        Edge edge3 = new Edge(graph1.getEnd(), endNode, "ε");
        Edge edge4 = new Edge(graph2.getEnd(), endNode, "ε");
        this.start = begNode;
        this.end = endNode;
        this.edges.addAll(graph1.getEdges());
        this.edges.addAll(graph2.getEdges());
        this.edges.add(edge1);
        this.edges.add(edge2);
        this.edges.add(edge3);
        this.edges.add(edge4);
    }

    public void addUnion(Character characterOne, Character characterTwo) {
        Node nodebeg = new Node();
        Node nodeend = new Node();
        Edge edgeOne = new Edge(nodebeg, nodeend, characterOne.toString());
        Edge edgeTwo = new Edge(nodebeg, nodeend, characterTwo.toString());
        edges.add(edgeOne);
        edges.add(edgeTwo);
        start = nodebeg;
        end = nodeend;
    }

    public void addConcat(Character character, Graph graph) {
        Node begNode = new Node();
        Edge edge = new Edge(begNode, graph.getStart(), character.toString());
        this.edges.addAll(graph.getEdges());
        this.edges.add(edge);
        this.start = begNode;
        this.end = graph.getEnd();
    }

    public void addConcat(Graph graph, Character character) {
        Node endNode = new Node();
        Edge edge = new Edge(graph.getEnd(), endNode, character.toString());
        this.edges.addAll(graph.getEdges());
        this.edges.add(edge);
        this.start = graph.getStart();
        this.end = endNode;
    }

    public void addConcat(Graph graph1, Graph graph2) {
        Edge edge = new Edge(graph1.getEnd(), graph2.getStart(), "ε");
        this.start = graph1.getStart();
        this.end = graph2.getEnd();
        this.edges.addAll(graph1.getEdges());
        this.edges.addAll(graph2.getEdges());
        this.edges.add(edge);
    }

    public void addConcat(Character characterOne, Character characterTwo) {
        Node begNode = new Node();
        Node midNode = new Node();
        Node endNode = new Node();
        Edge edge1 = new Edge(begNode, midNode, characterOne.toString());
        Edge edge2 = new Edge(midNode, endNode, characterTwo.toString());
        this.start = begNode;
        this.end = endNode;
        this.edges.add(edge1);
        this.edges.add(edge2);
    }

    @Override
    public String toString() {
        StringBuilder printString = new StringBuilder("Start=" + this.start + "  End=" + this.end + "\n");
        for (int i = 0; i < edges.size(); i++) {
            printString.append(edges.get(i)).append("\n");
        }
        return printString.toString();
    }
}

3.3 核心逻辑实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
public class Regex {
    private String regex;
    private Stack<Character> operatorStack;
    private Stack operandStack;
    private int[][] priority = {
            // *&|()#
            { 1, 1, 1,-1, 1, 1},
            {-1, 1, 1,-1, 1, 1},
            {-1,-1, 1,-1, 1, 1},
            {-1,-1,-1,-1, 0, 2},
            { 1, 1, 1, 1, 1, 1},
            {-1,-1,-1,-1,-1,-1}
    };

    public Regex() {
        regex = "";
        operatorStack = new Stack<>();
        operandStack = new Stack<>();
    }

    public Regex(String _regex) {
        regex = "";
        operatorStack = new Stack<>();
        operandStack = new Stack<>();
        prepareString(_regex);
    }

    /**
     * 核心转换代码
     * stack 记录 NFA 片段
     * 依次读取表达式的每个字符 ch
     * 如果 ch 是运算符，从 stack 出栈所需数目的 NFA 片段，构建新的 NFA 片段后入栈 stack
     * 如果 ch 是普通字符，创建新的状态，并构建只包含此状态的 NFA 片段入栈 stack
     * 返回 stack 栈顶的 NFA 片段，即最终结果
     */
    public NFA transformNFA() {
        if (regex.length() == 0)
            return null;
        else {
            int i = 0;
            operatorStack.push('#');
            char[] _regex = (regex + "#").toCharArray();
            while (_regex[i] != '#' || operatorStack.peek() != '#') {
                if (!isOperator(_regex[i])) {
                    operandStack.push(_regex[i]);
                    i++;
                } else {
                    int value = priorityOperator(operatorStack.peek(), _regex[i]);
                    switch (value) {
                        case 1:
                            Character character = operatorStack.pop();
                            switch (character) {
                                case '*':
                                    Object obj = operandStack.pop();
                                    Graph graph1 = new Graph();
                                    graph1.Star(obj);
                                    operandStack.push(graph1);
                                    break;
                                case '&':
                                    Object obj2 = operandStack.pop();
                                    Object obj1 = operandStack.pop();
                                    Graph graph2 = new Graph();
                                    graph2.Concat(obj1, obj2);
                                    operandStack.push(graph2);
                                    break;
                                case '|':
                                    Object obj4 = operandStack.pop();
                                    Object obj3 = operandStack.pop();
                                    Graph graph3 = new Graph();
                                    graph3.Union(obj3, obj4);
                                    operandStack.push(graph3);
                                    break;
                                default:
                                    break;
                            }
                            break;
                        case 0:
                            operatorStack.pop();
                            i++;
                            break;
                        case -1:
                            operatorStack.push(_regex[i]);
                            i++;
                            break;
                        default:
                            break;
                    }
                }
            }
            Graph graph = (Graph) operandStack.pop();
            System.out.println("====================process====================");
            System.out.println(graph);
            NFA nfa = new NFA();
            nfa.setS(getS(graph.getEnd().getId()));
            nfa.setCigama(getCigama(regex));
            nfa.setConvert(getConvert(graph));
            nfa.setS0(getS0(graph.getStart().getId()));
            nfa.setF(getF(graph.getEnd().getId()));
            return nfa;
        }
    }

    private List<Integer> getF(int id) {
        List<Integer> list = new ArrayList<>();
        list.add(id);
        return list;
    }

    private String[][] getConvert(Graph graph) {
        int n = graph.getEnd().getId() + 1;
        String[][] convert = new String[n][n];
        for (String[] tmp : convert) {
            Arrays.fill(tmp,"");
        }
        for(int i = 0; i < n; i++){
            convert[i][i] = "ε";
        }
        for (int i = 0; i < graph.getEdges().size(); i++) {
            int beginId = graph.getEdges().get(i).getBegin().getId();
            int endId = graph.getEdges().get(i).getEnd().getId();
            convert[beginId][endId] += graph.getEdges().get(i).getLabel();
        }
        return convert;
    }

    private List<Integer> getS0(int id) {
        List<Integer> list = new ArrayList<>();
        list.add(id);
        return list;
    }

    private List<Integer> getS(int cnt) {
        List<Integer> list = new ArrayList<>();
        for (int i = 0; i <= cnt; i++) {
            list.add(i);
        }
        return list;
    }

    private char[] getCigama(String regex) {
        char[] chars = regex.toCharArray();
        List<Character> list = new ArrayList<>();
        for (int i = 0; i < chars.length; i++) {
            if(chars[i]=='(' || chars[i]==')' || chars[i]=='*' || chars[i]=='|' || chars[i]=='&'){
                continue;
            }
            if(!list.contains(chars[i])){
                list.add(chars[i]);
            }
        }
        char[] cigama = new char[list.size()];
        for (int i = 0; i < list.size(); i++) {
            cigama[i] = list.get(i);
        }
        return cigama;
    }

    public void reset(){
        Node.reset();
        operandStack.clear();
        operatorStack.clear();
    }

    public String getRegex() {
        return regex;
    }

    public void setRegex(String _regex) {
        prepareString(_regex);
    }

    private boolean isOperator(Character character) {
        String operatorString = "*&|()#";
        if (operatorString.contains(character.toString())) {
            return true;
        } else {
            return false;
        }
    }

    private int priorityOperator(Character character1, Character character2) {
        String priorityString = "*&|()#";
        return this.priority[priorityString.indexOf(character1.toString())][priorityString
                .indexOf(character2.toString())];
    }

    /**
     * 在构建 NFA 之前，需要对正则表达式进行处理，以 (a|b)*abb 为例，在正则表达式里是没有连接符号的，这时就需要添加连接符
     * 对当前字符类型进行判断，并对前一个字符进行判断，最终得到添加连接符之后的字符串
     * 如 (a|b)*abb 添加完则为 (a|b)*&a&b&b
     */
    private void prepareString(String _regex) {
        char[] regexs = _regex.replaceAll(" ", "").toCharArray();
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < regexs.length; i++) {
            if (i == 0)
                sb.append(regexs[i]);
            else {
                if (regexs[i] == '|' || regexs[i] == '*' || regexs[i] == ')') {
                    sb.append(regexs[i]);
                } else {
                    if (regexs[i - 1] == '(' || regexs[i - 1] == '|')
                        sb.append(regexs[i]);
                    else
                        sb.append("&" + regexs[i]);
                }
            }
        }
        regex = sb.toString();
    }

}

3.4 定义测试类Main

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public class Main {
    public static void main(String[] args) {
        String regexExp = "(ab|c)*abb";
        System.out.println("待转换的正则表达式：" + regexExp);
        System.out.println("====================preprocess====================");
        Regex regex = new Regex(regexExp);
        System.out.println("预处理后的表达式："+regex.getRegex());
        NFA nfa = regex.transformNFA();
        print(nfa);
        regex.reset();
        DFA dfa = new NTD().definite(nfa);
        print("dfa", dfa);
        DFA mfa = new MinDFA().minDFA(dfa);
        print("mfa",mfa);
    }
    static void print(String tagName, DFA dfa){
        System.out.println("===================="+tagName+"====================");
        System.out.print("DFA状态集：");            DisplayUtils.displayS(dfa);
        System.out.print("DFA字母表：");            DisplayUtils.displayCigama(dfa);
        System.out.print("DFA状态转换函数：");       DisplayUtils.displayConvert(dfa);
        System.out.print("DFA唯一初态：");          DisplayUtils.displayS0(dfa);
        System.out.print("DFA终态集：");            DisplayUtils.displayF(dfa);
    }

    static void print(NFA nfa){
        System.out.println("===================="+ "nfa" +"====================");
        System.out.print("NFA状态集：");            DisplayUtils.displayS(nfa);
        System.out.print("NFA字母表：");            DisplayUtils.displayCigama(nfa);
        System.out.print("NFA状态转换函数：");       DisplayUtils.displayConvert(nfa);
        System.out.print("NFA初态集：");            DisplayUtils.displayS0(nfa);
        System.out.print("NFA终态集：");            DisplayUtils.displayF(nfa);
    }
}

输出结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
待转换的正则表达式：(ab|c)*abb
====================preprocess====================
预处理后的表达式：(a&b|c)*&a&b&b
====================process====================
Start=5  End=9
Edge [begin=0, end=1, label=a]
Edge [begin=1, end=2, label=b]
Edge [begin=3, end=0, label=ε]
Edge [begin=2, end=4, label=ε]
Edge [begin=3, end=4, label=c]
Edge [begin=5, end=6, label=ε]
Edge [begin=5, end=3, label=ε]
Edge [begin=4, end=6, label=ε]
Edge [begin=4, end=3, label=ε]
Edge [begin=6, end=7, label=a]
Edge [begin=7, end=8, label=b]
Edge [begin=8, end=9, label=b]

====================nfa====================
NFA状态集：[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
NFA字母表：[a, b, c]
NFA状态转换函数：0a1  1b2  2ε4  3ε0  3c4  4ε3  4ε6  5ε3  5ε6  6a7  7b8  8b9  
NFA初态集：[5]
NFA终态集：[9]
====================process====================
原状态：[3, 5, 6, 0]	新状态：[1, 7]	转换函数：0a1;	[0, 3, 4, 6]	转换函数：0c2;	
原状态：[1, 7]	新状态：[0, 2, 3, 4, 6, 8]	转换函数：1b3;	
原状态：[0, 3, 4, 6]	新状态：[1, 7]	转换函数：2a1;	[0, 3, 4, 6]	转换函数：2c2;	
原状态：[0, 2, 3, 4, 6, 8]	新状态：[1, 7]	转换函数：3a1;	[9]	转换函数：3b4;	[0, 3, 4, 6]	转换函数：3c2;	
原状态：[9]	新状态：
====================dfa====================
DFA状态集：[0, 1, 2, 3, 4]
DFA字母表：[a, b, c]
DFA状态转换函数：0a1	0c2	1b3	2a1	2c2	3a1	3c2	3b4	
DFA唯一初态：0
DFA终态集：[4]
====================final groups====================
0:[4]
1:[0, 2]
2:[1]
3:[3]
====================mfa====================
DFA状态集：[0, 1, 2, 3]
DFA字母表：[a, b, c]
DFA状态转换函数：1c1	1a2	2b3	3b0	3c1	3a2	
DFA唯一初态：1
DFA终态集：[0]

可在草稿纸上做出对应MFA进行检验，尝试多组案例观察结果是否正确

以上则是编译原理实验：正则表达式->NFA->DFA->MFA 实现的全部内容啦！

-------------本文结束感谢您的阅读-------------