八数码游戏
1. 八数码简介
八数码问题也称为九宫问题。在3×3的方格棋盘上,摆有八个棋子,每个棋子上标有1至8的某一数字,不同棋子上标的数字不相同。棋盘上还有一个空格,与空格相邻的棋子可以移到空格中。
要求解决的问题是:给出一个初始状态和一个目标状态,找出一种从初始转变成目标状态的移动棋子的步骤。
所谓问题的一个状态就是棋子在棋盘上的一种摆法。解八数码问题实际上就是找出从初始状态到达目标状态所经过的一系列中间过渡状态。
2. 八数码问题的状态空间法表示
2.1. 状态定义
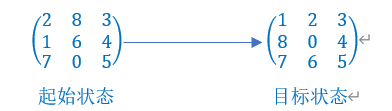
利用矩阵存储每一步的状态,空位用0表示,例如起始状态为:
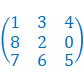
目标状态为:
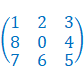
2.2. 方向符号定义
搜索时按照URDL的顺序:
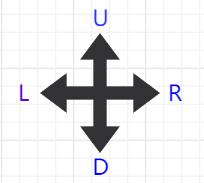
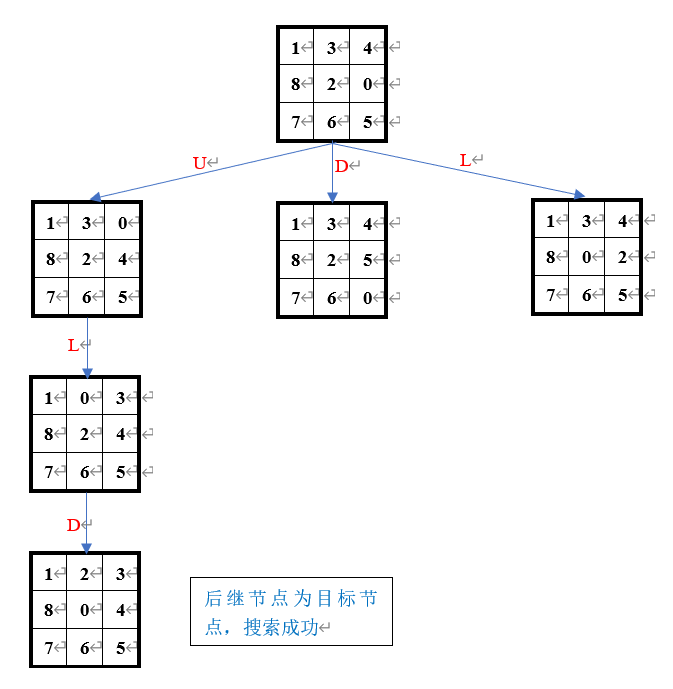
2.3. 从初始状态到目标状态的求解过程
例:下图为宽度优先搜索算法对应具体搜索路径:
3. 八数码问题的盲目搜索技术概述
3.1. dfs、bfs算法基本原理简要介绍
3.1.1 深度优先搜索
按照一条路径一直往下深度延伸子节点的算法,直到找到答案为止(由于本实验中数字组合相对较少,不考虑内存超限的情况)。在深度优先搜索的求解过程中使用Stack来存储还未搜索的节点,已经搜索过的节点使用一个链表来存储(避免重复的搜索)。如果已经在链表中那么就不在放到栈中,因为之前已经搜索过了,故不需要重复搜索。
3.1.2 宽度优先搜索
以接近起始节点的程度依次扩展节点的搜索技术(即:离起始节点近的节点先被扩展),在这个过程中使用Queue来存储其中还没有遍历的但是已经发展了的节点,同时使用链表来存储已经搜索过的子节点,然后基本上是和深度优先搜索算法类似。
扩展节点的原则:先扩展出来的节点之后会优先被扩展(生成其所有的后继节点)
3.2. dfs、bfs算法流程图
3.2.1 深度优先搜索算法步骤
① 把起始节点 S 放到未扩展节点的 OPEN 表(此时OPEN表是一个堆栈,后进先出)中。如果此节点为一目标节点,则得到解
② 如果 OPEN 为一空表,则无解、失败退出
③ 把第一个节点(记作节点 n )从 OPEN 表移到 CLOSED 表
④ 如果节点 n 的深度等于最大深度,则转向②
⑤ 扩展节点 n ,产生其全部后继节点,并把它们放入 OPEN 表的前头。如果没有后继节点,则转向②
⑥ 如果后继节点中有任一个节点为目标节点,则求得一个解(反向追踪从目标节点到起始节点的路径),成功退出;否则,转向②
3.2.2 深度优先搜索算法的流程图
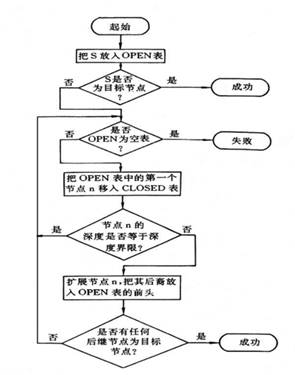
3.2.3 宽度优先搜索算法步骤
① 把起始节点放到 OPEN 表中(如果该起始节点为一目标节点,则得到解)
② 如果 OPEN 是个空表,则无解,失败退出;否则继续下一步
③ 把第一个节点(记作节点 n )从 OPEN 表移出,并把它放入 CLOSED 的已扩展节点表中
④ 扩展节点 n 。如果没有后继节点,则转向第②步
⑤ 把 n 的所有后继节点放到OPEN表的末端,并提供从这些后继节点回到 n 的指针(记录每一个节点的父节点信息)
⑥ 如果 n 的任一后继节点是个目标节点,则找到一个解(反向追踪得到从目标节点到起始节点的路径),成功退出,否则转向第②步
3.2.4 宽度优先搜索算法的流程图
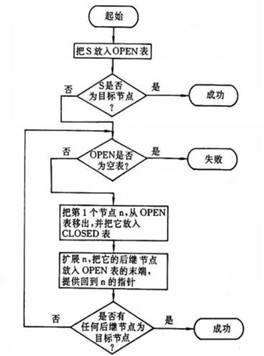
4. 八数码问题的启发式搜索技术
4.1. 启发式搜索原理
启发式搜索就是在状态空间中的搜索对每一个搜索的位置进行评估,得到最好的位置,再从这个位置进行搜索直到目标。这样可以省略大量无谓的搜索路径,提高了效率。在启发式搜索中,对位置的估价是十分重要的。采用了不同的估价可以有不同的效果。
4.2. 估价函数
用f(n)来表示节点n的估价函数,公式表示为: f(n)=g(n)+h(n),其中:
f(n) 是从初始状态经由状态n到目标状态的代价估计,称作估价函数
d(n) 是在状态空间从初始状态到状态n的实际代价,称作节点深度
h(n) 是从状态n到目标状态的的估计代价,称作启发函数
4.3. 估价函数设计
估价函数是由两部分构成的,节点深度d(n)其实就是当前已经走的步数,不用额外设计函数;启发函数h(n)是比较重要的一个部分,启发函数的设计直接影响了估计函数的效率,有几种定义方法:
当前节点与目标节点差异的度量 => 当前结点与目标节点相比,位置不符的数字个数
当前节点与目标节点距离的度量 => 当前结点与目标节点格局位置不符的数字移动到目标节点中对应位置的最短距离之和
每一对逆序数字的某倍数,位置不符的数字个数的总和+逆序数的三倍
这里选择的是第一种,计算当前节点与目标节点相比,有多少个数字的位置不符
4.4. 算法描述
① 把起始节点S放到OPEN表中,并计算节点S的;
② 如果OPEN是空表,则失败退出(无解);
③ 从OPEN表中选择一个f值最小的节点i。如果有几个节点值相同,当其中有一个为目标节点时,则选择目标节点;否则就选择其中任一个节点作为节点i;
④ 把节点 i 从 OPEN 表中移出,并把它放入 CLOSED 的已扩展节点表中
⑤ 如果 i 是个目标节点,则成功退出(有解)
⑥ 扩展节点 i ,生成其全部后继节点。对于 i 的每一个后继节点 j :
⑦ 转向②
4.5. 算法流程图
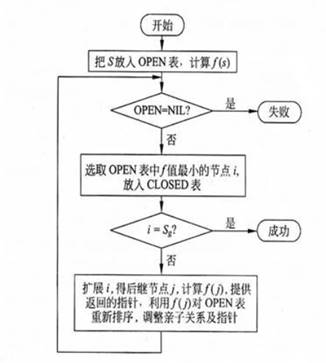
5.案例及分析
5.1. 取2.1中的例子

| 算法 | 步数 | 操作符 | OPEN表 大小 | CLOSED表 大小 | CPU运行时间(ms) |
|---|---|---|---|---|---|
| 宽度优先搜索 | 3 | ULD | 5 | 5 | 2 |
| 深度优先搜索 | 3 | ULD | 1 | 47 | 5 |
| 启发式搜索 | 3 | ULD | 1 | 3 | 62 |
程序运行结果截图(考虑输出过程的时间):
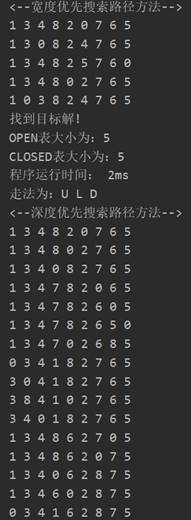
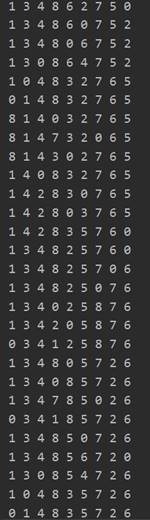
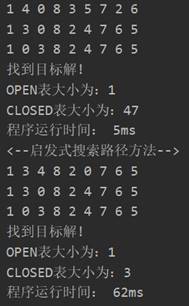
5.2. 其他测试的例子(简单)
| 算法 | 步数 | 操作符 | OPEN表 大小 | CLOSED表 大小 | CPU运行时间(ms) |
|---|---|---|---|---|---|
| 宽度优先搜索 | 5 | UULDR | 15 | 21 | 3 |
| 深度优先搜索 | 5 | UULDR | 2 | 55 | 5 |
| 启发式搜索 | 5 | UULDR | 1 | 5 | 67 |
程序运行结果截图(考虑输出过程的时间):
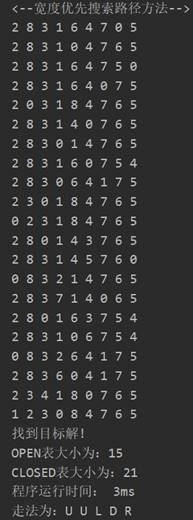
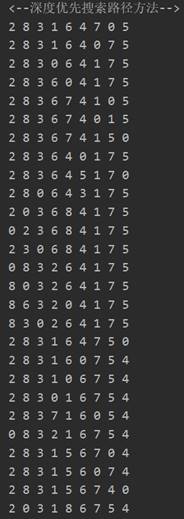

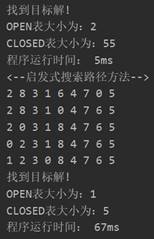
5.3. 其他测试的例子(复杂)

| 算法 | 步数 | 操作符 | OPEN表 大小 | CLOSED表 大小 | CPU运行时间(ms) |
|---|---|---|---|---|---|
| 宽度优先搜索 | 16 | URDRUULLDRRDLLUR | 4280 | 6856 | 808 |
| 深度优先搜索 | 16 | URDRUULLDRRDLLUR | 9 | 4597 | 211 |
| 启发式搜索 | 16 | URDRUULLDRRDLLUR | 1 | 567 | 57 |
程序运行结果截图(不输出过程,故不考虑打印结果所用时间):

6.体会与致谢
通过这次实验,我对八数码问题的宽、深度优先搜索有了更深入的了解,同时也习得了启发式搜索的思想。在此也十分感谢老师课程PPT的制作及课上课下的指导,下面谈谈我遇到的问题和收获。
综合不同的测试数据结果来看,程序运行时间从小到大的顺序为:启发式搜索、深度优先搜索(确保深度界限满足条件)、宽度优先搜索
宽度优先搜索方法能够保证在搜索树中找到一条通向目标节点的最短途径(所用操作符最少),只要结点间可以到达,就一定可以找到一个最优解。
深度优先搜索如果不设置深度界限将会耗时特别长,如果深度界限设置的太小则可能导致缺解现象,如果设置的很巧妙则搜索速度很快,综合看来十分不稳定,如何定义一个较好的深度界限有待进一步思考。
在经过大量随机初始化九宫格的实验后,发现启发式搜索更加实用有效,能在较复杂情况下求得更加优质的解,但是对于估价函数的定义趋向多元化,如何更好地定义一个估价函数有待深入讨论。
缺陷和不足:
- 在进行随机初始化九宫格的多次实验时,出现宽度优先搜索和深度优先搜索耗时过长而无结果输出的问题,但启发式搜索可以很好的输出结果;
- 只做了宽度优先搜索的提供追踪解,可以输出从初始状态到目标状态的操作符顺序。
- 未讨论时间复杂性和空间复杂性。
7.实验程序简单说明
使用的语言是java,运行环境是IDEA,程序一共用到四个类:EightPuzzle、EightPuzzleMove、EightPuzzleAlgorithm、EightPuzzleMain。
(1)EightPuzzle:定义八数码的状态属性包括存放九宫格的二维数组data、深度depth,估价函数evaluation和启发函数mispositon。方法包括:isSame()判定二维数组data是否相同,进而重写方法equals(为了后面过滤掉重复状态);print()将二维数组data转成一维输出到控制台(为了节省空间);getBlankPositon()获取空格(0)的坐标;深拷贝depthClone();
(2)EightPuzzleMove:控制空格的移动,包括两个方法isMovable()判定是否可以继续移动(不能出边界)、move()通过输入的方向来进行相应的移动。
(3)EightPuzzleAlgorithm:主要包括三个算法bfs()宽度优先搜索、boundedDfs()有界限深度优先搜索、A_Star()启发式搜索;除此之外还有一些定义的状态信息、队列、栈、数组等。
(4)EightPuzzleMain:程序的入口,主要包括起始状态和末状态的输入、三种搜索算法的运行以及方法isSolvable()判断是否有解。
java代码参考github:EightPuzzle